Оглавление:
Производная функции 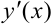 сама является функцией, которая также может иметь производную.
сама является функцией, которая также может иметь производную.
Второй производной называют производную от производной и обозначают 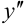 :
: 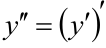 . Вторую производную также можно дифференцировать:
. Вторую производную также можно дифференцировать: 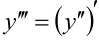 . В общем случае, производная
. В общем случае, производная 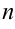 — го порядка определяется как производная от производной
— го порядка определяется как производная от производной 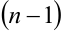 — го порядка:
— го порядка:
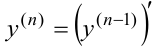
При повторном дифференцировании обычных функций вида 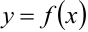 справедливы все правила дифференцирования и таблица производных.
справедливы все правила дифференцирования и таблица производных.
Производная второго порядка 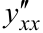 от функции заданной параметрически вычисляется по формуле
от функции заданной параметрически вычисляется по формуле
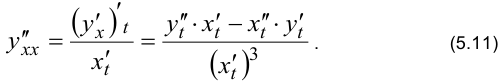
Пример:
Определить вторую производную функции. Для определения второй производной первую производную 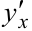 дифференцируем по
дифференцируем по 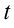 :
:
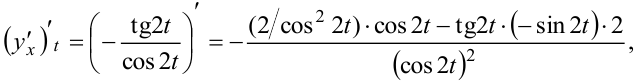
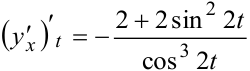 . Разделим полученное выражение на
. Разделим полученное выражение на 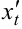 и найдём
и найдём 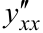 :
: 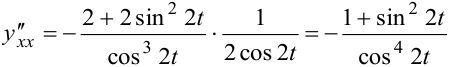 .
.
Пример выполнения задания
В задании требуется найти производную для различных функций. В пунктах а), b), с), d), е) используются приведенные выше правила дифференцирования и таблица производных.
В пункте а) заданная функция представляет из себя алгебраическую сумму функций, умноженных на постоянные величины. Для определения производной используются правила дифференцирования №1,3, 5 и таблица производных основных функций.
a) Найти производную функции
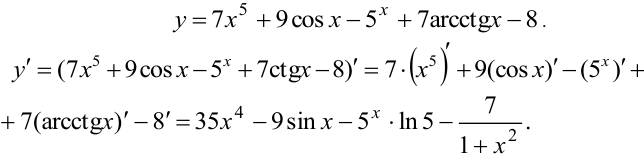
В пункте b) функция 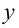 — произведение двух функций, для определения производной используется правило дифференцирования №4.
— произведение двух функций, для определения производной используется правило дифференцирования №4.
b) 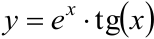 .
.
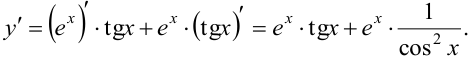
В пункте с) функция 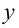 — частное двух функций. Для определения производной используется правило №6.
— частное двух функций. Для определения производной используется правило №6.
c) 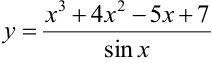 .
.
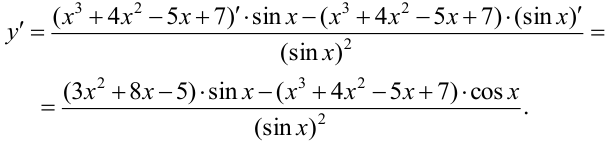
В пункте d) задана сложная функция, производная определяется по правилу №7.
d) 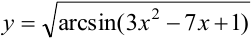 . Внешней функцией является корень квадратный (частный случай степенной функции), внутренняя функция — арксинус, которая является внешней для внутренней функции — квадратного трёхчлена.
. Внешней функцией является корень квадратный (частный случай степенной функции), внутренняя функция — арксинус, которая является внешней для внутренней функции — квадратного трёхчлена.
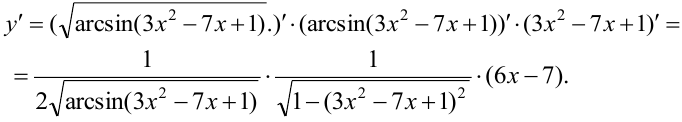
В пункте е) задана сложно — показательная функция. Для нахождения её производной применяется предварительное логарифмирование функции.
е) 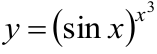
Логарифмируем левую и правую части по основанию е:
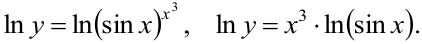
Теперь дифференцируем, учитывая, что 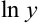 — сложная функция, т.к.
— сложная функция, т.к. 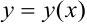 .
.
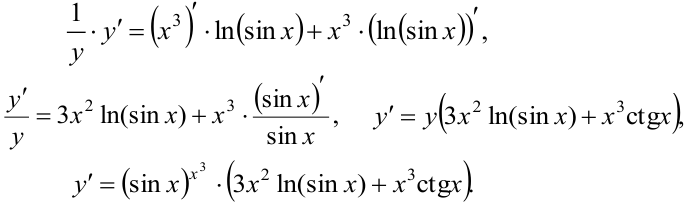
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:

