Две бесконечно малых 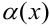 и
и 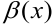 называются эквивалентными, если предел их дроби равен единице:
называются эквивалентными, если предел их дроби равен единице: 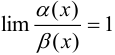 .
.
Запись 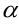 ~
~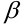 означает, что
означает, что 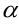 и
и 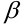 — эквивалентные бесконечно малые величины. Эквивалентные бесконечно малые величины обладают рядом свойств, которые описываются следующими теоремами.
— эквивалентные бесконечно малые величины. Эквивалентные бесконечно малые величины обладают рядом свойств, которые описываются следующими теоремами.
Теорема 1. Две бесконечно малые 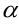 и
и 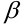 , эквивалентные порознь третьей бесконечно малой
, эквивалентные порознь третьей бесконечно малой 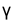 , эквивалентны между собой.
, эквивалентны между собой.
Теорема 2. Разность 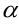 —
—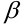 двух эквивалентных бесконечно малых является бесконечно малой высшего порядка малости по сравнению с каждой из них.
двух эквивалентных бесконечно малых является бесконечно малой высшего порядка малости по сравнению с каждой из них.
Теорема 3. Предел дроби двух бесконечно малых сохраняет своё значение при замене этих бесконечно малых им эквивалентными.
Теорема 4. Сумма бесконечно малых различных порядков эквивалентна слагаемому низшего порядка малости.
Слагаемое, эквивалентное всей сумме бесконечно малых, называется главной частью суммы. Замена суммы её главной частью называется «отбрасыванием» бесконечно малых высшего порядка малости.
При вычислении пределов используют эквивалентность следующих бесконечно малых: если 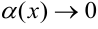 , то справедлива следующая таблица 1 соотношений эквивалентных бесконечно малых величин.
, то справедлива следующая таблица 1 соотношений эквивалентных бесконечно малых величин.

Кроме того, сумма бесконечно малых эквивалентна бесконечно малой низшего порядка малости, входящей в сумму. Так при 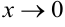
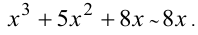
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Кратко о двух замечательных пределов |
| Сравнение бесконечно малых функций |
| Непрерывность функции |
| Производная. Геометрический смысл производной |
