Большую роль в математическом анализе имеет дробь двух бесконечно малых величин. Предел дроби может иметь разные значения. Всего существует четыре разных случая для предела дроби бесконечно малых величин 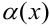 и
и 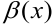 .
.
1. Если 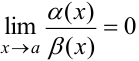 , то
, то 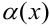 называется бесконечно малой высшего порядка малости по сравнению с
называется бесконечно малой высшего порядка малости по сравнению с 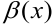 , при этом
, при этом 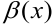 — бесконечно малая низшего порядка малости по сравнению с
— бесконечно малая низшего порядка малости по сравнению с 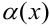 .
.
2. Если 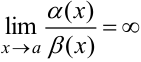 , то
, то 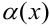 называется бесконечно малой низшего порядка малости по сравнению с
называется бесконечно малой низшего порядка малости по сравнению с 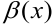 , при этом
, при этом 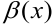 — бесконечно малая высшего порядка малости по сравнению с
— бесконечно малая высшего порядка малости по сравнению с 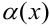 .
.
3. Если 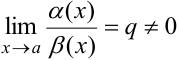 , то
, то 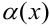 и
и 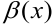 называется бесконечно малыми одного порядка малости.
называется бесконечно малыми одного порядка малости.
В частном случае, две бесконечно малых 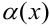 и
и 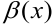 называются эквивалентными, если предел их дроби равен единице:
называются эквивалентными, если предел их дроби равен единице:
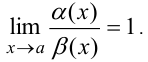
4. Если 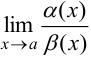 не существует, то
не существует, то 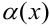 и
и 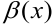 называется несравнимыми бесконечно малыми.
называется несравнимыми бесконечно малыми.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Свойства пределов в высшей математике |
| Кратко о двух замечательных пределов |
| Эквивалентные бесконечно малые величины: теоремы и таблица |
| Непрерывность функции |
