Оглавление:
Свойства пределов справедливы как для пределов числовых последовательностей, так и для пределов функций. Свойства справедливы как для 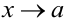 , так и для
, так и для 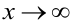 .
.
1. Предел суммы переменных равен сумме их пределов
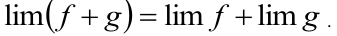
2. Предел произведения переменных равен произведению их пределов
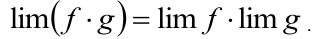
3. Предел дроби двух переменных равен дроби их пределу, если предел делителя отличен от нуля:
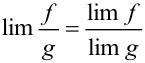 , если
, если 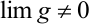 .
.
4. Постоянный множитель выносится за знак предела 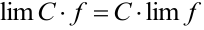 .
.
5. Предел постоянной равен самой постоянной, 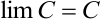 , где
, где 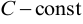 .
.
Примеры выполнения задания
Пример:
Найти пределы числовой последовательности (пункт а) и функций. В пункте б) воспользоваться первым замечательным пределом, в пункте в) — свойством эквивалентности бесконечно малых.
Решение:
Вычисление предела по каждому пункту рассмотрим на примерах
Пункт a)
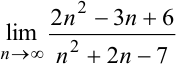 .
.
Решение:
В задачах этого пункта имеет место неопределённость вида 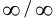 . Чтобы раскрыть неопределённость вида
. Чтобы раскрыть неопределённость вида 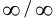 , нужно разделить числитель и знаменатель на наивысшую степень переменной, входящую в выражение. В результате, если многочлены числителя и знаменателя одинаковой степени, предел равен отношению старших коэффициентов числителя и знаменателя. Если в числителе степень многочлена выше, чем в знаменателе, то предел равен бесконечности. Если степень числителя ниже степени знаменателя, то предел равен нулю.
, нужно разделить числитель и знаменатель на наивысшую степень переменной, входящую в выражение. В результате, если многочлены числителя и знаменателя одинаковой степени, предел равен отношению старших коэффициентов числителя и знаменателя. Если в числителе степень многочлена выше, чем в знаменателе, то предел равен бесконечности. Если степень числителя ниже степени знаменателя, то предел равен нулю.
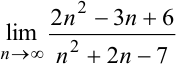 . При
. При 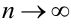 числитель и знаменатель дроби — бесконечно большие величины, неопределенность вида
числитель и знаменатель дроби — бесконечно большие величины, неопределенность вида 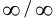 . Для раскрытия неопределённости разделим числитель и знаменатель на наибольшую степень переменной, то есть, разделим на
. Для раскрытия неопределённости разделим числитель и знаменатель на наибольшую степень переменной, то есть, разделим на 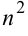 .
.
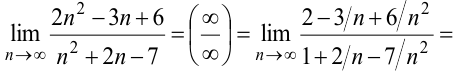
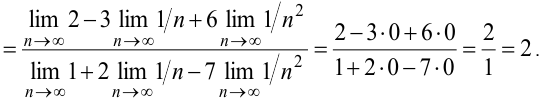
Пункт б)
Примеры вычисления пределов с помощью первого замечательного предела:
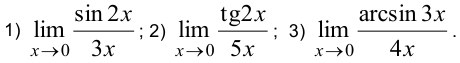
Решение:
Вычисляя числитель и знаменатель заданных пределов при  , получаем неопределенность вида
, получаем неопределенность вида 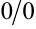 .
.
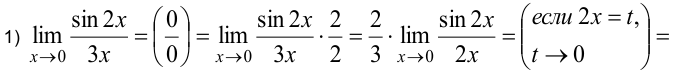
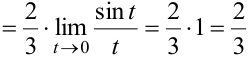 . Умножив числитель и знаменатель на 2, получили первый замечательный предел.
. Умножив числитель и знаменатель на 2, получили первый замечательный предел.
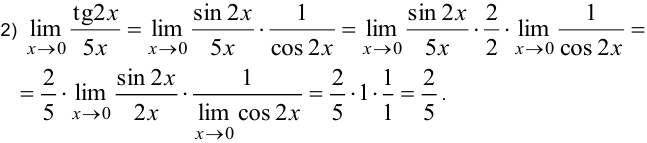
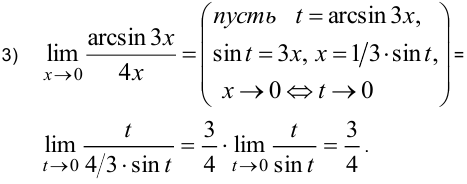
Пункт в)
Используя эквивалентность бесконечно малых величин, вычислить пределы: 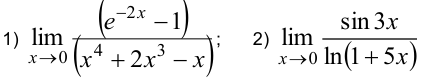 .
.
Решение:
При  величины
величины  . Алгебраическая сумма бесконечно малых
. Алгебраическая сумма бесконечно малых 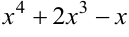 эквивалентна бесконечно малой низшего порядка малости (
эквивалентна бесконечно малой низшего порядка малости (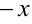 ). В числителе и знаменателе дробей — бесконечно малые величины. Согласно теореме 3, предел дроби двух бесконечно малых сохраняет своё значение при замене этих бесконечно малых им эквивалентными. Вычисляем пределы, заменяя бесконечно малые величины им эквивалентными, используя таблицу 1.
). В числителе и знаменателе дробей — бесконечно малые величины. Согласно теореме 3, предел дроби двух бесконечно малых сохраняет своё значение при замене этих бесконечно малых им эквивалентными. Вычисляем пределы, заменяя бесконечно малые величины им эквивалентными, используя таблицу 1.
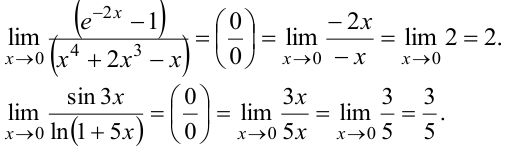
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Предел функции при x>∞ |
| Свойства бесконечно малых и бесконечно больших величин |
| Кратко о двух замечательных пределов |
| Сравнение бесконечно малых функций |

