Оглавление:
Скалярным произведением двух векторов называется число, равное произведению длин векторов на косинус угла между ними:
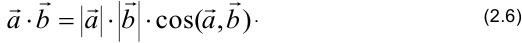
Свойства скалярного произведения
1. При перестановке сомножителей произведение не изменится: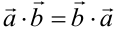 
. Это объясняется тем, что при перестановке скалярных множителей произведение не меняется 
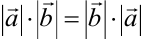, а также тем, что косинус — функция чётная: 
.
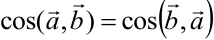2. Скалярный сомножитель (число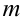 
) можно вынести за знак произведения: 
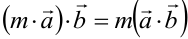. Это свойство — следствие свойства операции умножения вектора на число.
3. Скалярное произведение равно нулю, если хотя бы один из векторов нулевой или векторы перпендикулярны (так как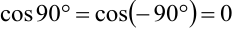 
).
4. Скалярный квадрат вектора равен квадрату его длины: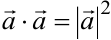 
(следует из того, что 
).
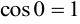5. Скалярное произведение обладает распределительным свойством: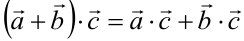 
.
Пусть векторы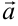 
, 
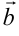заданы своими координатами: 
, 
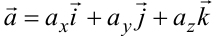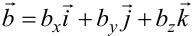. В силу свойств 2, 3, 4, 5 произведение 
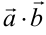можно вычислить как произведение многочлена на многочлен. С учетом того, что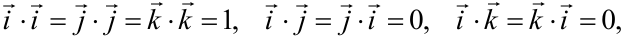 
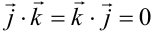, скалярное произведение векторов равно сумме произведений одноименных координат:
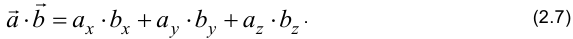
Из свойства 3 и формулы (2.7) следует условие перпендикулярности двух векторов:
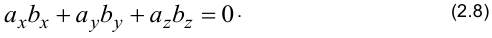
Из формулы (2.6) следует формула для определения угла между векторами (с учетом формул (2.7) и (2.2)):
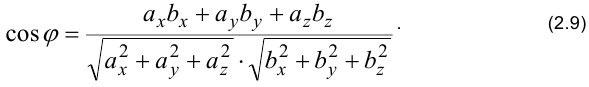
Физическое приложение скалярного произведения
Если материальная точка, на которую действует сила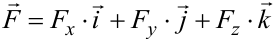 
двигается по вектору 
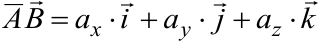, то работа 
силы 
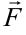по перемещению точки по направленному отрезку 
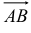равна скалярному произведению
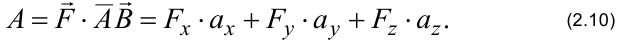
Пример выполнения задания
Пример:
Вычислить работу силы 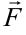(2,3,5) при перемещении материальной точки из положения (-2,0,-3) в положение 
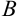(1,4,-2). (Предполагаются согласованные единицы силы и перемещения).
Решение:
Найдём координаты вектора 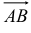как разность координат точки конца вектора и точки начала:
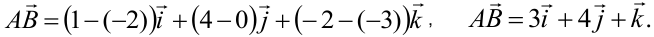
Работу вычисляем по формуле (2.10):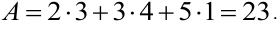 
Ответ: = 23 (единиц работы).
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
