Оглавление:
Геометрическим вектором называется направленный отрезок или упорядоченная пара точек (точка начала и точка конца вектора). Обозначается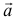 
, 
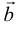или 
.
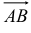Два геометрических вектора называются коллинеарными, если существует прямая линия, которой они параллельны.
Три геометрических вектора называются компланарными, если существует плоскость, которой они параллельны.
Два вектора называются равными, если они коллинеарные, одинаковой длины и направлены в одну сторону. Основываясь на этом определении, у вектора можно менять точку начала. Такие вектора называются свободными, перемещение векторов ничем не ограничено. При этом три компланарных вектора будут лежать в одной плоскости.
Длина вектора (модуль вектора) обозначается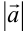 
или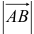 
.
Умножение вектора на число, сложение векторов
Умножение вектора на число и сложение векторов относятся к линейным операциям с векторами.
Умножение вектора на число
Результатом умножения вектора 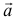на число 
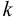является вектор 
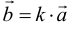. При этом векторы 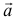, 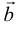коллинеарные и сонаправленные при 
и направлены в разные стороны при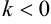 
. Длина полученного вектора 
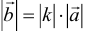. Если 
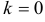, получается нулевой вектор (нуль-вектор 
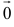), направление которого не определено. Если 
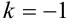, то векторы 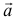и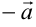 
называют противоположными.
Свойства операции умножения вектора на число:
1) для любых чисел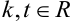 
и вектора 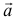справедливо равенство
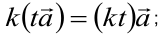
2) если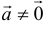 
, то для любого коллинеарного ему вектора 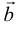существует только одно число , такое, что .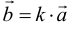
Сложение векторов
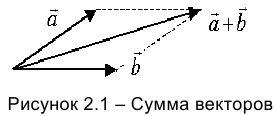
Сложение двух векторов можно провести методом параллелограмма. При этом точки начала векторов совмещаются, на векторах достраивается параллелограмм. Диагональ параллелограмма — сумма векторов (рисунок 2.1).
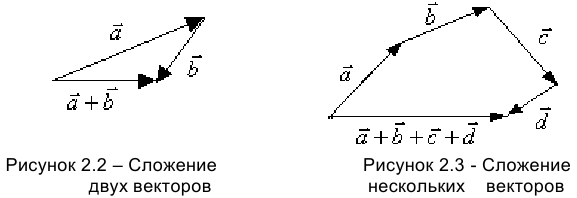
При другом методе сложения двух векторов точка начала второго вектора помещается в конец первого вектора. Замыкающий вектор является суммой (рисунок 2.2). При сложении нескольких векторов строится векторный многоугольник, в котором замыкающий вектор является суммой (рисунок 2.3).
Свойства операции сложения векторов
1) операция обладает свойством коммутативности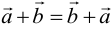 
;
2) сложение векторов ассоциативно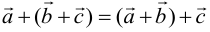 
;
3) сложение дистрибутивно по отношению к умножению на число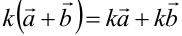 
;
4) для любых чисел 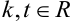и вектора 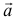выполняется равенство
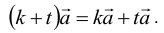
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
