Пусть в матрице  размера
размера 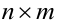 выбраны произвольно
выбраны произвольно 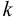 строк и
строк и 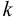 столбцов
столбцов 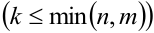 . Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу порядка
. Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу порядка 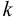 , определитель которой называется минором
, определитель которой называется минором 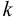 — го порядка матрицы
— го порядка матрицы  .
.
Например, в матрице  имеются миноры 1-го, 2-го и 3-го порядков:
имеются миноры 1-го, 2-го и 3-го порядков:
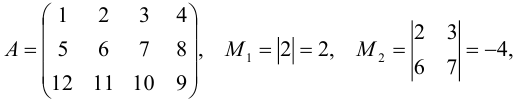 и т.д.,
и т.д.,
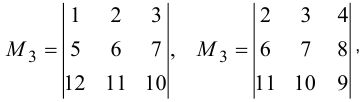 и т.д.
и т.д.
Максимальный порядок 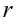 отличных от нуля миноров матрицы
отличных от нуля миноров матрицы  называется её рангом, а любой минор порядка
называется её рангом, а любой минор порядка 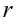 , отличный от нуля, называется базисным. Ранг матрицы
, отличный от нуля, называется базисным. Ранг матрицы  обозначается
обозначается 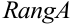 .
.
Пример:
Определить ранг матрицы 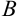 ,
,
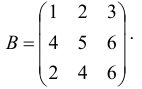
Решение:
Матрица имеет один минор 3-го порядка:
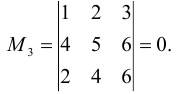
Минор 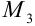 равен нулю, так как элементы первой и третьей строк пропорциональны.
равен нулю, так как элементы первой и третьей строк пропорциональны.
Миноров второго порядка несколько. Некоторые из них не равны нулю:
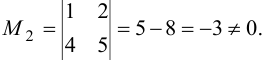
Следовательно, ранг матрицы равен двум.
Ответ: 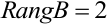 .
.
Примечание — в примере 1.6 ранг матрицы определяется простым перебором миноров. Однако существуют специальные методы определения ранга матрицы, например, метод элементарных преобразований, и другие.
С понятием ранга матрицы связан критерий существования решений общих линейных систем алгебраических уравнений. Под общими системами понимаются системы, в которых число уравнений может не совпадать с числом неизвестных, а также такие системы, в которых определитель матрицы системы равен нулю.
Будем рассматривать общую систему 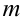 линейных уравнений с
линейных уравнений с 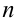 неизвестными
неизвестными  :
:
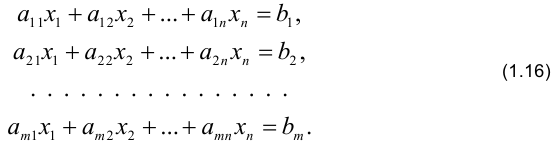
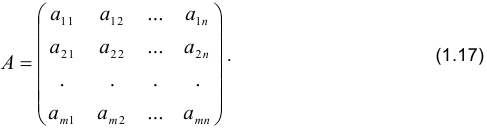
Матрица системы  состоит из коэффициентов при неизвестных:
состоит из коэффициентов при неизвестных:
Если в матрице системы добавить столбец свободных членов, то полученную матрицу называют расширенной матрицей системы 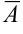 :
:
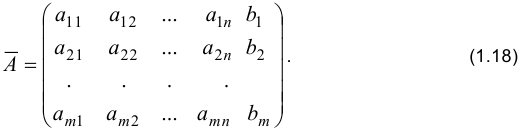
Критерий существования решений системы (1.16) или, иначе, критерий совместности системы выражен теоремой Кронекера — Капелли.
Теорема. Система уравнений (1.16) совместна (имеет решение) тогда и только тогда, когда ранг матрицы  равен рангу расширенной матрицы
равен рангу расширенной матрицы 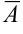 .
.
Следствие теоремы Кронекера — Капелли: если 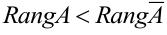 , то система (1.16) несовместна и решений не имеет.
, то система (1.16) несовместна и решений не имеет.
Неравенство 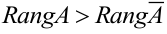 невозможно, так как добавление столбца в матрице не может привести к уменьшению её ранга.
невозможно, так как добавление столбца в матрице не может привести к уменьшению её ранга.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Решение определенных систем с помощью правила Крамера |
| Решение систем с помощью метода Гаусса |
| Векторы. Линейные операции над векторами |
| Разложение вектора по базису: определение и пример с решением |

