Оглавление:
Метод Гаусса
Метод Гаусса — универсальный метод решения систем линейных алгебраических уравнений. Он в отличие от выше рассмотренных методов может быть использован и при решении систем, когда число неизвестных не равно числу уравнений. Метод состоит из двух этапов. При «прямом ходе» последовательно уменьшают количество неизвестных в уравнениях системы. При этом можно каждое уравнение умножать на число, не равное нулю, складывать и переставлять уравнения. При «обратном ходе» непосредственно вычисляются значения неизвестных.
Пример:
Решить систему алгебраических уравнений методом Гаусса
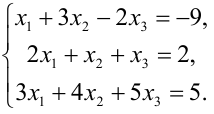
Решение:
При умножении уравнений на число, не равное нулю, сложении и перестановке уравнений все изменения происходят с коэффициентами уравнений и свободными членами, поэтому для решения достаточно записать матрицу из коэффициентов и свободных членов. Такая матрица называется расширенной матрицей системы.
Расширенная матрица системы это матрица, в которой к матрице системы справа добавлен столбец свободных членов. Для заданной системы уравнений расширенная матрица имеет вид:
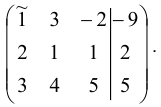
В первом столбце выбираем ведущий элемент (помечен сверху волнистой чертой), с помощью которого «обнуляем» элементы первого столбца. Умножив первую строку на (-2), прибавим её ко второй строке. Умножив первую строку на (-3), прибавим её к третьей строке. Этим добиваемся того, что в первом столбце элементы ниже первого равны нулю. Затем выбираем во второй строке ведущий элемент (коэффициент — 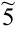 ), с помощью которого «обнуляем» элемент, стоящий во втором столбце внизу. Для этого умножаем вторую строку на (-1) и прибавляем её к третьей строке. Результат вычислений:
), с помощью которого «обнуляем» элемент, стоящий во втором столбце внизу. Для этого умножаем вторую строку на (-1) и прибавляем её к третьей строке. Результат вычислений:
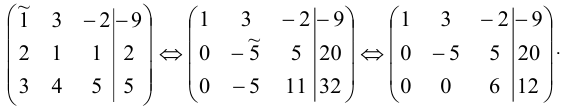
На этом прямой ход метода Гаусса закончен, система уравнений приняла треугольный вид:
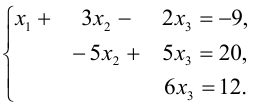
Из последнего уравнения определяем 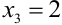 и подставляем это значение во второе уравнение, получим
и подставляем это значение во второе уравнение, получим 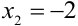 . Из первого уравнения определяем
. Из первого уравнения определяем 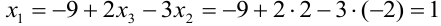 .
.
Ответ: 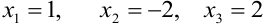 .
.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:

