Пусть задана система 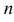 уравнений с
уравнений с 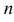 неизвестными величинами
неизвестными величинами  вида:
вида:
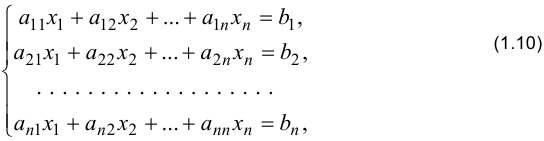
где  называются коэффициентами при неизвестных,
называются коэффициентами при неизвестных, 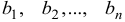 называются правыми частями системы (свободными членами).
называются правыми частями системы (свободными членами).
Все неизвестные величины  входят в систему в первой степени и образуют с коэффициентами линейную комбинацию. Такая система уравнений называется линейной системой алгебраических уравнений, порядок системы определяется величиной
входят в систему в первой степени и образуют с коэффициентами линейную комбинацию. Такая система уравнений называется линейной системой алгебраических уравнений, порядок системы определяется величиной 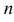 .
.
Введём для системы (1.10) следующие обозначения:
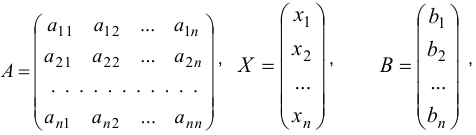
где  — квадратная матрица, называется матрицей системы (1.10);
— квадратная матрица, называется матрицей системы (1.10); 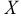 — матрица-столбец неизвестных;
— матрица-столбец неизвестных; 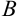 — матрица-столбец свободных членов.
— матрица-столбец свободных членов.
Если определитель квадратной матрицы  не равен нулю, т. е. матрица
не равен нулю, т. е. матрица  не вырожденная, то система (1.10) называется определенной. Решение определенных систем можно получить с помощью обратной матрицы.
не вырожденная, то система (1.10) называется определенной. Решение определенных систем можно получить с помощью обратной матрицы.
С учетом введенных обозначений систему (1.10) можно записать в виде матричного уравнения

Умножаем обе части уравнения (1.11) на обратную матрицу:
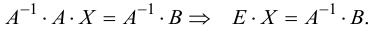
Окончательно, решение уравнения (1.10) имеет вид:

Остаётся найти обратную матрицу 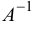 и умножить её на матрицу
и умножить её на матрицу 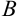 . В результате получим решение системы (1.12). В этом состоит матричный метод решения систем алгебраических уравнений (метод обратной матрицы).
. В результате получим решение системы (1.12). В этом состоит матричный метод решения систем алгебраических уравнений (метод обратной матрицы).
Пример:
Дана система линейных алгебраических уравнений третьего порядка:
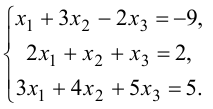
Найти решение системы уравнений методом обратной матрицы.
Решение:
Вычислим определитель системы:
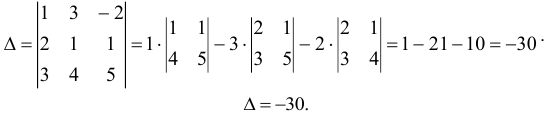
Матрица системы невырожденная и имеет обратную матрицу.
Определяем алгебраические дополнения элементов матрицы системы:
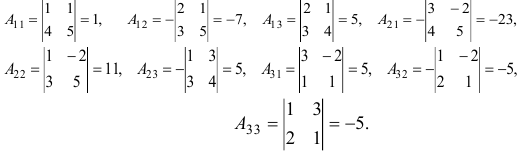
Решение системы уравнений определяем по формуле (1.12), где обратная матрица 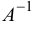 составляется по формуле (1.9):
составляется по формуле (1.9):
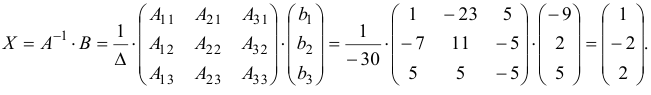
Ответ: 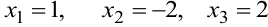 .
.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:

