1. Две матрицы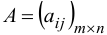 
и 
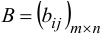одинаковой структуры (одинаковых размеров) равны друг другу, если их соответствующие элементы равны. Понятие неравенства в матрицах не определено.
2. Две матрицы одинаковой размерности можно складывать и вычитать:
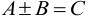. При этом 
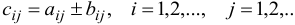. Здесь 
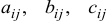— элементы матриц 
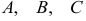, стоящие на одинаковых местах. Например,
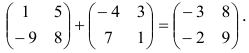
3. Произведение матрицы 
на число (скаляр) 
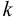определяется соотношением 
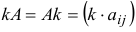. Каждый элемент матрицы умножается на это число: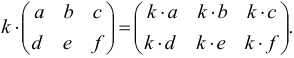 
4. Операция замены строк матрицы столбцами с теми же номерами называется транспонированием матрицы. Эта операция обозначается так:
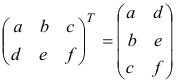. Повторное транспонирование приводит к исходной матрице: 
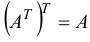. Матрицы, удовлетворяющие условию 
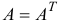, называются симметрическими. Они характеризуются
условием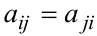 
. Пример симметрических матриц: 
.
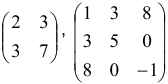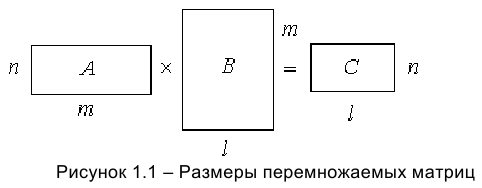
5. Две матрицы согласованных размеров можно перемножить. Количество столбцов (длина строки) первой матрицы должно быть равно количеству строк (высоте столбца) второй:
На рисунке 1.1 указаны размеры перемножаемых матриц и результата.
Для расчета элемента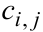 
элементы строки 
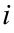матрицы перемножаются с элементами столбца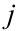 
матрицы 
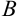по формуле:
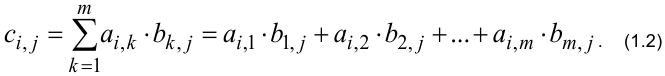
Приведём пример, из которого несложно понять правило умножения матриц:
Пример:
Перемножить матрицы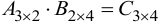 
.
Решение:
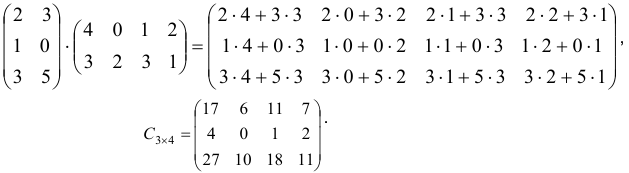
В приведённом примере нельзя сомножители (матрицы) поменять местами, потому что их размеры будут не согласованы. Но и в общем случае произведение матриц некоммутативное, то есть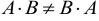 
.
Если же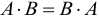 
, то матрицы и 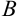называются коммутативными.
При умножении матрицы на согласованную по размерам единичную матрицу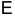 
матрица не изменяется: 
. Это означает, что в матричной алгебре единичная матрица играет роль единицы обычной алгебры: при умножении числа на единицу результат равен исходному числу. Например,
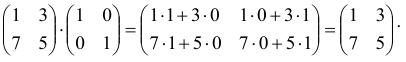
Свойство ассоциативности в матричной алгебре сохраняется. Это означает, что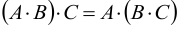 
.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
