Оглавление:
Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях.
Случайное явление — это такое явление, которое при неоднократном воспроизведении одного и того же опыта каждый раз протекает несколько по иному.
Рассмотрим примеры:
- Одно и то же тело несколько раз взвешивается на аналитических весах; результаты повторных взвешиваний несколько отличаются друг от друга. Результат зависит от положения тела на чашечке весов, случайные вибрации аппарата, ошибки отсчета показаний прибора и т.д.
- Самолет совершает полет на заданной высоте; теоретически он летит горизонтально, фактически полет совершается отклонениями центра массы самолета, связанным турбулентностью атмосферы.
При изучении явлений «точными науками» применяемых в физике, технике, механике, явление идеализируется, упрощается, выделяются самые главные, основные факторы; влиянием остальных, второстепенных факторов просто пренебрегают.
Практика показывает, что, наблюдая за массой однородных случайных явлений, мы обычно обнаруживаем в них вполне определенные закономерности, своего рода устойчивости, свойственные именно массовым случайным явлениям.
Например, если много раз подряд бросить монету, частота появления герба (отношение числа появившихся гербов к общему числу бросаний) постепенно стабилизируется, приближаясь к вполне определенному числу, равному 1/2, хотя каждое отдельное событие заранее неопределенное, случайное.
Закономерности, проявляются в этой массе, оказываются практически независимыми от индивидуальных особенностей отдельных случайных явлений, входящих в массу. Эти отдельные особенности в массе как бы взаимно погашаются, и средний результат массы случайных явлений оказывается практически уже не случайным. Именно эта устойчивость массовых случайных явлений и служит базой для применения вероятностных, статистических методов исследования.
Событие. Вероятность события
Каждая наука содержит ряд основных понятий, на которых она базируется. В геометрии — это понятия точки, прямой, линии. В механике — силы, массы, скорости и т.д. Основные понятия существуют и в теории вероятностей.
Это событие. Под событием в теории вероятностей понимается всякий факт, который в результате опыта может произойти или не произойти.
Пример: а) появления герба при бросании монеты, б) появление трех гербов при трехкратном бросании монеты, в) появление туза при вынимании карты из колоды.
Эти события обладает той или иной степенью возможности. Чтобы количественно сравнить между собой события по степени их возможности, очевидно, нужно с каждым событием связать определенное число, которое тем больше, чем более возможно событие. Такое число мы назовем вероятностью события -это второе основное понятие теории вероятностей.
Вероятность события есть численная мера степени объективной возможности этого события.
Сравнивая между собой различные события по степени их возможности, мы должны установить единицу измерения. В качестве такой единицы примем вероятность достоверного события, т.е. событие, которое в результате опыта непременно должно произойти.
Пример: выпадение не более 6 очков при бросании одной игральной кости.
Противоположностью по отношению к достоверному событию является невозможное событие, т.е. такое событие, которое в данном опыте не может произойти.
Пример: появление 12 очков при бросании одной игральной кости. Вероятность невозможного события равна нулю.
Случайным событием является событие, которое в результате опыта может либо произойти, либо не произойти. Вероятность 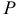 случайного события находится в интервале [0, 1].
случайного события находится в интервале [0, 1].
То или иное событие осуществляется при отдельной совокупности условий. Эту «совокупность условий» будем называть испытанием. Таким образом, событие будет рассматриваться как результат испытания.
Например, стрелок стреляет по мишени. Выстрел — это испытание. Попадание в мишень — это событие.
Несколько событий образуют полную группу, если в результате испытания появиться хотя бы одно из них, т. е. появление хотя бы одного из событий полной группы есть достоверное событие.
Если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий.
Например, стрелок произвел выстрел по цели. Обязательно произойдет одно из следующих двух событий: попадание, промах. Эти два несовместные события образуют полную группу.
События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.
Например, появление герба и надписи при бросании монеты — равновозмож-ные события; появление того или иного числа очков на брошенной игральной кости — равновозможные события.
Классическое определение вероятности
Несколько событий называются несовместными в данном опыте, если никакие два из них не могут появиться вместе.
Например, выпадение герба и цифры при одном бросании монеты; попадание и промах при одном выстреле.
Существуют группы событий, обладающие тремя свойствами: 1) образуют полную группу; 2) несовместны; 3) равновозможны.
Например, появление герба и цифры при бросании монеты; появление числа очков 1,2, … ,6 при бросании игральной кости.
События, образующие такую группу, называются случаями (шансами). Случай называется благоприятным событием, если появление этого случая влечет за собой появление данного события. Если опыт сводится к схеме случаев, то вероятность события 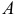 в данном опыте можно оценить по относительной доле благоприятных событий:
в данном опыте можно оценить по относительной доле благоприятных событий: 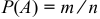 , где
, где 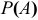 — вероятность события
— вероятность события 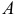 ,
, 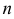 — общее число случаев;
— общее число случаев; 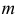 — число случаев благоприятных событию
— число случаев благоприятных событию 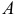 . Так как
. Так как 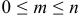 , то
, то 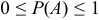 .
. 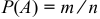 — классическое определение вероятностей.
— классическое определение вероятностей.
Пример №1
В урне находится 2 белых и 3 черных шара. Из урны наугад вынимается один шар. Требуется найти вероятность того, что этот шар будет белый.
Решение:
Пусть 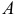 событие, состоящее в появлении белого шара. Общее число случаев
событие, состоящее в появлении белого шара. Общее число случаев 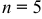 , число случаев, благоприятных событию
, число случаев, благоприятных событию 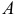 ,
, 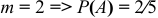 .
.
Пример №2
Набирая номер телефона. Абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.
Решение:
Пусть 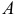 событие — набрана нужная цифра. Общее число элементарных исходов равно 10, т.е.
событие — набрана нужная цифра. Общее число элементарных исходов равно 10, т.е. 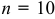 . Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятное событие лишь:
. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятное событие лишь: 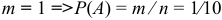 .
.
Основные формулы комбинаторики
Комбинаторика изучает количество комбинаций, подчиненных определенным условиям, которые можно составить из элементов заданного конечного множества. Приведем основные формулы комбинаторики:
Перестановками называются комбинации, состоящие из одних и тех же 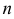 различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок:
различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок: 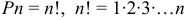 . Напомним, что 0! = 1.
. Напомним, что 0! = 1.
Пример №3
Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз.
Решение:
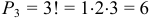 .
.
Размещениями называются комбинации, составленные из 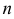 различных элементов по
различных элементов по 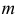 элементов, которые отличаются либо составом элементов, либо их порядком.
элементов, которые отличаются либо составом элементов, либо их порядком.
Число всех возможных размещений 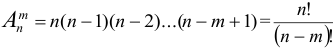
Пример №4
Сколько можно составить сигналов из 5 флажков различного цвета, взятых по 2.
Решение:
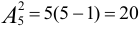 .
.
Сочетаниями называют комбинации, составленные из 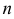 различных элементов по
различных элементов по 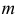 элементов, которые отличаются хотя бы одним элементом. Число сочетаний:
элементов, которые отличаются хотя бы одним элементом. Число сочетаний: 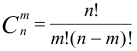 .
.
Пример №5
Сколькими способами можно выбрать две детали из ящика, содержащего 5 деталей?
Решение:
Искомое число способов 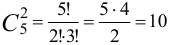 .
.
Числа размещений, перестановок и сочетаний связаны равенством:
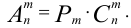
При решении задач комбинаторики используют правила:
Правило суммы. Если некоторый объект 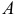 может быть выбран из совокупности объектов
может быть выбран из совокупности объектов 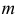 способами, а другой объект
способами, а другой объект 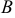 может быть выбран
может быть выбран 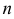 способами, то выбрать либо
способами, то выбрать либо 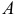 , либо
, либо 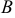 , можно
, можно 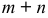 способами.
способами.
Правило произведения. Если объект 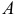 можно выбрать из совокупности объектов
можно выбрать из совокупности объектов 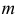 способами и после каждого такого выбора объект
способами и после каждого такого выбора объект 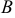 можно выбрать
можно выбрать 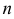 способами, то пара объектов
способами, то пара объектов 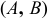 в указанном порядке может быть выбрана
в указанном порядке может быть выбрана 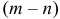 способами.
способами.
Пример №6
Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их на удачу. Найти вероятность того, что набраны нужные цифры.
Решение:
Пусть 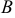 — это событие благоприятное т.е. набраны нужные две цифры. Всего можно набрать столько различных чисел, сколько может быть составлено размещений из десяти цифр по две, т.е.
— это событие благоприятное т.е. набраны нужные две цифры. Всего можно набрать столько различных чисел, сколько может быть составлено размещений из десяти цифр по две, т.е. 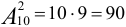 . Общее число исходов будет 90. Эти исходы несовместны, равновозможны и образуют полную группу
. Общее число исходов будет 90. Эти исходы несовместны, равновозможны и образуют полную группу 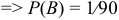 .
.
Пример №7
В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди шести взятых наудачу деталей 4 стандартные.
Решение:
Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т.е. числу сочетаний из 10 элементов по 6 элементов 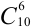 .
.
Определим число исходов, благоприятствующих событию А (среди шести деталей 4 стандартные). Четыре стандартные детали можно взять из 7 стандартных 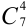 способами, при этом остальные 6-4 = 2 детали должны быть нестандартными, 2 нестандартные детали из 10-7 = 3 детали можно
способами, при этом остальные 6-4 = 2 детали должны быть нестандартными, 2 нестандартные детали из 10-7 = 3 детали можно 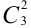 способами. Следовательно, число благоприятных событий равно произведению
способами. Следовательно, число благоприятных событий равно произведению 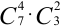 .
.
Вероятность 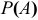 равно отношению благоприятствующих событий, к числу всех исходов.
равно отношению благоприятствующих событий, к числу всех исходов.
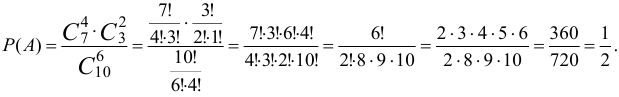
Статистическое и геометрическое определение вероятности
Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике часто встречаются испытания, число возможных исходов которых бесконечно. В таких случаях классическое определение неприменимо. В качестве статистической вероятности события принимают относительную частоту или число, близкое к ней.
Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. 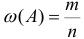 , где
, где 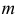 — число появлений события,
— число появлений события, 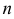 — общее число испытаний.
— общее число испытаний.
Отличие вероятности от относительной частоты: вероятность вычисляют до опыта, а относительную частоту — после опыта.
Если опытным путем установлена относительная частота, то полученное число можно принять за приближенное значение вероятности.
Недостатком статистического определения является неоднозначность статистической вероятности.
Под геометрической вероятностью понимают вероятность попадания точки в область (отрезок, часть плоскости, фигуру…).
Пример №8
Партия из 20 деталей содержит одну нестандартную. Какова вероятность, что при случайной выборке 10 деталей из этой партии все они будут стандартные?
Решение:
Число всех случайных способов выбора 10 деталей 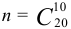 , а число благоприятствующих событий
, а число благоприятствующих событий 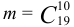 . Искомая вероятность
. Искомая вероятность
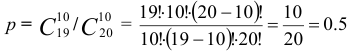
Пример №9
В партии из 200 изделий обнаружено 8 нестандартных. Определить относительную частоту появления стандартных изделий.
Решение. Относительная частоту появления стандартных изделий
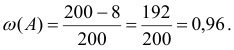
Теорема сложения вероятностей несовместных событий
Суммой 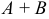 двух событий
двух событий 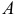 и
и 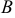 называют событие, состоящие в появлении события
называют событие, состоящие в появлении события 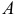 , или событии
, или событии 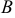 , или обоих этих событий.
, или обоих этих событий.
Например, если из орудия произведены два выстрела и 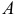 — попадание при первом выстреле,
— попадание при первом выстреле, 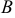 — попадание при втором выстреле, то
— попадание при втором выстреле, то 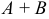 — попадание при первом выстреле, или при втором выстреле, или в обоих выстрелах.
— попадание при первом выстреле, или при втором выстреле, или в обоих выстрелах.
Суммой нескольких событий называется событие, которое состоит в появлении хотя бы одного из этих событий.
Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
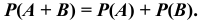
Следствие. Вероятность появления одного из нескольких парно несовместных событий, безразлично какого, равна сумме вероятностей этих событий.
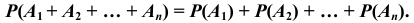
Пример №10
В урне 20 шаров: 8 красных, 6 синих, 6 белых. Найти вероятность появления цветного шара.
Решение:
Появление цветного шара означает появление либо красного, либо синего шара. Вероятность появления красного 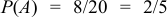 , синего
, синего 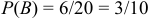 . События
. События 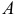 и
и 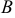 несовместимы, по теореме сложения
несовместимы, по теореме сложения
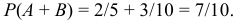
Пример №11
В лотерее 1000 билетов: из них на один билет падает выигрыш 500 руб, на 10 билетов — выигрыш по 100 руб, на 80 билетов — 20 руб, на 100 билетов — 8 руб, остальные невыигрышные. Найти вероятность выигрыша не менее 20 руб при покупке 1 билета.
Решение:
Событие 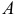 — выиграть не менее 20 руб. Событие
— выиграть не менее 20 руб. Событие 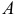 может осуществиться, если наступит одно из несовместных событий:
может осуществиться, если наступит одно из несовместных событий: 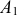 — выигрыш 20 руб,
— выигрыш 20 руб, 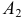 — 100 руб,
— 100 руб, 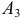 — 500 руб. События несовместимы, следовательно,
— 500 руб. События несовместимы, следовательно, 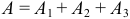 . По теореме сложения вероятностей несовместных событий
. По теореме сложения вероятностей несовместных событий
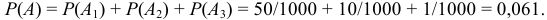
Теорема. Сумма вероятностей событий 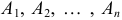 образующих полную группу, равна единице:
образующих полную группу, равна единице: 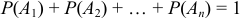 .
.
Пример №12
Круговая мишень состоит из трех зон: I, II, III. Вероятность попадания в первую зону при одном выстреле — 0,15, во вторую — 0,23, в третью -0,17. Найти вероятность промаха.
Решение:
Событие 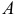 — промах, противоположное событие
— промах, противоположное событие 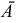 — попадание. Событие
— попадание. Событие 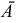 может осуществиться, если наступит одно из несовместных событий:
может осуществиться, если наступит одно из несовместных событий: 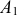 — попадание в первую зону,
— попадание в первую зону, 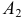 — во вторую,
— во вторую, 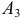 — в третью. События несовместимы, следовательно
— в третью. События несовместимы, следовательно 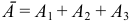 . По теореме сложения:
. По теореме сложения:
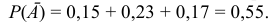
Событие 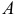 и
и 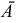 образуют полную группу, следовательно,
образуют полную группу, следовательно, 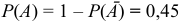 .
.
Теорема. Сумма вероятностей противоположных событий равна единице: 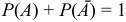 .
.
Теорема умножения вероятностей
Произведением двух событий 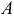 и
и 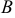 называют событие
называют событие 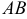 , состоящее в совместном появлении этих событий. Например, если
, состоящее в совместном появлении этих событий. Например, если 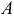 — деталь годная,
— деталь годная, 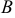 — деталь стальная, то
— деталь стальная, то 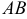 — деталь годная и стальная.
— деталь годная и стальная.
Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если 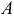 ,
, 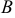 и
и 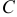 — появление «герба» в первом, во втором и третьем бросаниях монеты, то
— появление «герба» в первом, во втором и третьем бросаниях монеты, то 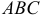 — выпадение «герба» во всех трех испытаниях.
— выпадение «герба» во всех трех испытаниях.
Условной вероятностью 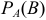 называют вероятность события
называют вероятность события 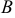 , вычисленную в предположении, что событие
, вычисленную в предположении, что событие 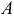 уже наступило и выражается по формуле
уже наступило и выражается по формуле
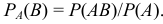
Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
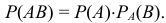
Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
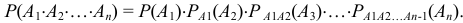
Для трех событий 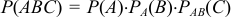 . Порядок, в котором расположены события, может быть выбран любым
. Порядок, в котором расположены события, может быть выбран любым
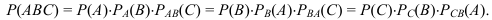
Пример №13
В урне 2 белых и 3 черных шара. Из урны вынимают подряд два шара. Найти вероятность того, что оба шара белые.
Решение:
Событие 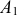 — извлечение белого шара при первом испытании,
— извлечение белого шара при первом испытании, 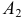 — извлечение белого шара при втором испытании. Эти события совместны, следовательно извлечение двух белых шаров
— извлечение белого шара при втором испытании. Эти события совместны, следовательно извлечение двух белых шаров 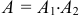 . Всего в урне 5 шаров. Вероятность извлечение белого шара при первом испытании
. Всего в урне 5 шаров. Вероятность извлечение белого шара при первом испытании 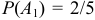 , вероятность извлечение белого шара при втором испытании при условии, что при первом испытании был извлечен белый шар
, вероятность извлечение белого шара при втором испытании при условии, что при первом испытании был извлечен белый шар 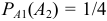 . По теореме умножения совместных событий
. По теореме умножения совместных событий 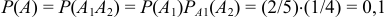 .
.
Независимые события. Теорема умножения для независимых событий
Событие 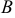 называют независимым от события
называют независимым от события 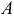 , если появление события
, если появление события 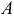 не изменяет вероятности события
не изменяет вероятности события 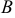 , т.е.
, т.е.
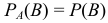
Если событие 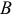 не зависит от события
не зависит от события 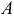 , то и событие
, то и событие 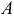 не зависит от события
не зависит от события 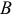 .
.
Теорема. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
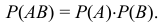
Несколько событий называют попарно независимыми, если каждые два из них независимы.
События 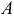 ,
, 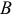 ,
, 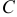 попарно независимы, если
попарно независимы, если 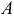 и
и 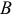 ,
, 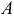 и
и 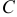 ,
, 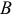 и
и 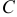 независимы.
независимы.
Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных.
Следствие 1. Вероятность совместного появления нескольких независимых событий, независимых в совокупности, равна произведению вероятностей этих событий:
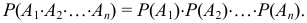
Следствие 2. Если события 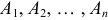 независимы, то противоположные им события
независимы, то противоположные им события 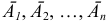 так же независимы.
так же независимы.
Пример №14
Производится три выстрела по одной и той же мишени. Вероятность попадания при первом, втором и третьем выстрелах равна 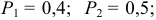
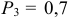 . Найти вероятность того, что в результате этих трех выстрелов произойдет ровно одно попадание.
. Найти вероятность того, что в результате этих трех выстрелов произойдет ровно одно попадание.
Решение:
Событие 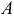 — ровно одно попадание в мишень;
— ровно одно попадание в мишень; 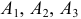 — попадание при первом, втором и третьем выстрелах соответственно;
— попадание при первом, втором и третьем выстрелах соответственно; 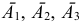 — промах при первом, втором и третьем выстрелах соответственно. Событие
— промах при первом, втором и третьем выстрелах соответственно. Событие 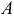 может наступить, если первый стрелок попал, а второй и третий не попали
может наступить, если первый стрелок попал, а второй и третий не попали 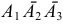 ; если второй стрелок попал, а первый и третий не попали
; если второй стрелок попал, а первый и третий не попали 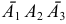 ; если третий стрелок попал, а первый и второй не попали
; если третий стрелок попал, а первый и второй не попали 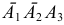 :
:
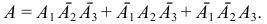
Искомая вероятность
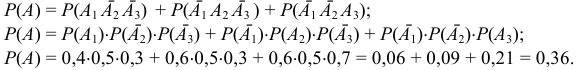
Вероятность появления хотя бы одного события
Теорема. Вероятность появления хотя бы одного из независимых событий 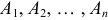 равна разности между единицей и произведением вероятностей противоположных событий
равна разности между единицей и произведением вероятностей противоположных событий 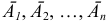 :
:
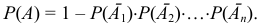
Следствие. Если событие 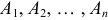 имеют одинаковую вероятность, равную
имеют одинаковую вероятность, равную 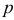 , то вероятность появления хотя бы одного из этих событий:
, то вероятность появления хотя бы одного из этих событий:
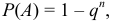
где 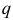 — вероятность противоположного события.
— вероятность противоположного события.
Пример №15
В типографии имеется 3 машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,8. Найти вероятность того, что в данный момент работает хотя бы одна машина.
Решение:
Событие 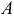 — машина работает, противоположное событие
— машина работает, противоположное событие 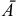 — машина не работает. Эти события образуют полную группу.
— машина не работает. Эти события образуют полную группу.
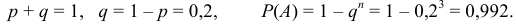
Теорема сложения вероятностей совместных событий
Два события называют совместными, если появление одного из них не исключает появление другого в одном и том же опыте.
Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.
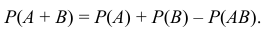
‘Замечание 1. Если два события независимы, то:
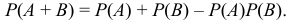
Замечание 2. Если два события зависимы, то:
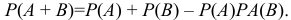
Замечание 3. Если два события несовместимы, то:
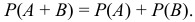
Пример №16
Вероятность попадания в цель при стрельбе первого и второго орудий соответственно равны 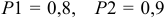 . Найти вероятность попадания при одновременном залпе (из обоих орудий) хотя бы одним из орудий.
. Найти вероятность попадания при одновременном залпе (из обоих орудий) хотя бы одним из орудий.
Решение:
Рассмотрим два способа решения:
1. По условию события 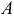 (попадание первого орудия) и
(попадание первого орудия) и 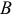 (попадание второго орудия) совместны и независимы. Вероятность того, что оба орудия попали
(попадание второго орудия) совместны и независимы. Вероятность того, что оба орудия попали
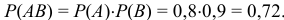
Вероятность попадания при одновременном залпе хотя бы одним из орудий
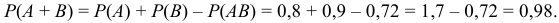
2. Так как события 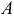 и
и 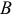 независимы, то вероятность появления хотя бы одного из этих событий вычислим по формуле
независимы, то вероятность появления хотя бы одного из этих событий вычислим по формуле
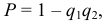
где 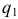 и
и 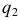 вероятности событий, противоположных событиям
вероятности событий, противоположных событиям 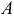 и
и 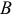
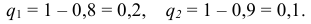
Вероятность появления хотя бы одного события:
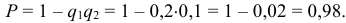
Формула полной вероятности
Теорема. Вероятность события 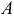 , которое может наступить лишь при условии появления одного из несовместных событий
, которое может наступить лишь при условии появления одного из несовместных событий 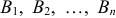 , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события
, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события 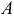 :
:
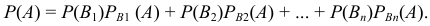
Пример №17
Имеется две группы людей. Вероятность того, что человек из первой группы будет партийный, равна 0,4, а второй — 0,6. Найти вероятность того, что выбранный наудачу человек является партийным.
Решение:
Человек может быть выбран либо из первой группы (событие 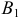 ) либо из второй группы (событие
) либо из второй группы (событие 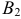 ). Вероятность того, что человек выбран из первого группы
). Вероятность того, что человек выбран из первого группы 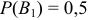 , из второй —
, из второй — 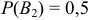 .
.
Условная вероятность выбора из первой группы партийного 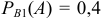 , из второй —
, из второй — 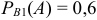 .
.
Вероятность выбора на удачу партийного человека вычислим по формуле полной вероятности:
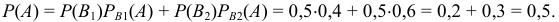
Вероятность гипотез. Формулы Бейса
Пусть событие 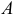 может наступить при условии появления одного из несовместных событий
может наступить при условии появления одного из несовместных событий 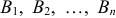 , образующих полную группу.
, образующих полную группу.
Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами.
Вероятность появления события 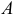 определяется по формуле полной вероятности:
определяется по формуле полной вероятности:
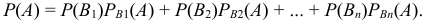
Допустим, что произведено испытание, в результате которого появилось событие 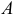 . Выясним, как изменились вероятности гипотез после того, как появилось событие
. Выясним, как изменились вероятности гипотез после того, как появилось событие 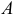 .
.
По теореме умножения имеем 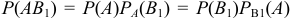 . Выражая
. Выражая 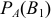 , получим
, получим 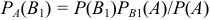 . Используя формулу полной вероятности, получим
. Используя формулу полной вероятности, получим
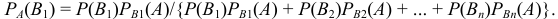
По аналогии
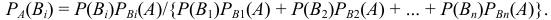
Полученные формулы называют формулами Бейса (по имени английского математика).
Формулы Бейса позволяют переоценить вероятность гипотез после того, как становится известным результат испытания, в итоге которого появилось событие 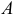 .
.
Пример №18
Для участия в спортивных студенческих соревнованиях, выделено из первой группы — 4, из второй — 6, из третьей — 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадёт в сборную института, равны соответственно 0,9, 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. Какой группе вероятнее всего принадлежит этот студент?
Решение:
Всего 15 студентов. Вероятность выбора из первой группы 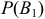 равна 4/15; из второй группы
равна 4/15; из второй группы 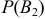 равна 6/15; из третьей группы
равна 6/15; из третьей группы 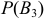 равна 5/15.
равна 5/15.
Вероятность попадания в сборную 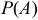 вычислим по формуле полной вероятности:
вычислим по формуле полной вероятности:
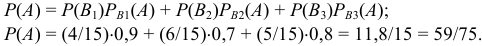
Найдём вероятность того, что выбранный студент попал в сборную из первой группы: 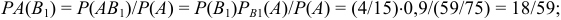
из второй 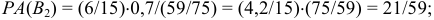
из третьей 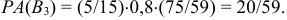
Ответ: вероятнее всего студент принадлежит второй группе.
Формула Бернулли
Если происходит несколько испытаний, причем вероятность события 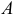 в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события
в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события 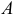 .
.
Пусть производиться 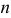 независимых испытаний, в каждом из которых событие
независимых испытаний, в каждом из которых событие 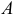 может появиться либо не появиться. Вероятность события в каждом испытании одна и та же, равная
может появиться либо не появиться. Вероятность события в каждом испытании одна и та же, равная 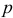 . Вероятность не наступления события в каждом испытании
. Вероятность не наступления события в каждом испытании 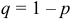 .
.
Вычислим вероятность 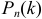 того, что при
того, что при 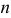 испытаниях событие
испытаниях событие 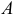 осуществляется ровно
осуществляется ровно 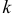 раз и не осуществляется
раз и не осуществляется 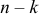 раз по формуле Бернулли:
раз по формуле Бернулли:
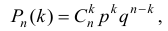
где 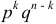 — умножение вероятностей независимых событий;
— умножение вероятностей независимых событий; 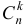 — столько можно составить сочетаний из
— столько можно составить сочетаний из 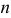 элементов и
элементов и 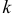 элементов.
элементов.
Пример №19
В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент: а) включено 4 мотора; б) включены все моторы; в) выключены все моторы.
Решение:
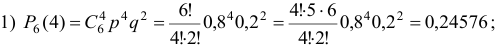
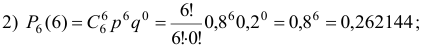
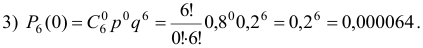
Локальная теорема Лапласа
Пользоваться формулой Бернулли при больших значениях 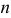 достаточно трудно, т.к. формула требует выполнения действий над очень большими числами.
достаточно трудно, т.к. формула требует выполнения действий над очень большими числами.
Например, если 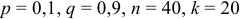 , то вероятность того, что при
, то вероятность того, что при 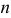 испытаниях событие
испытаниях событие 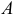 осуществляется ровно
осуществляется ровно 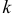 раз и не осуществляется
раз и не осуществляется 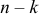 раз
раз 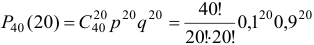 . При вычислении можно пользоваться специальными таблицами логарифмов факториалов, но из-за округлений в итоге окончательный результат может значительно отличаться от истинного.
. При вычислении можно пользоваться специальными таблицами логарифмов факториалов, но из-за округлений в итоге окончательный результат может значительно отличаться от истинного.
Локальная теорема Лапласа. Если вероятность 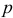 появления события
появления события 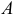 в каждом испытании постоянна и отлична от нуля и единицы, то вероятность
в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 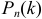 того, что событие
того, что событие 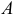 появиться в
появиться в 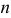 испытаниях ровно
испытаниях ровно 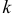 раз, приближенно равна (тем точнее, чем больше
раз, приближенно равна (тем точнее, чем больше 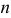 ) значению функции:
) значению функции:
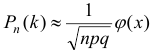 , где
, где 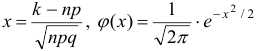 .
.
Функция 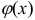 четная:
четная: 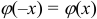 .
.
Пример №20
Найти вероятность того, что при 400 испытаниях событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2.
Решение:
По условию 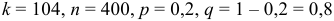 . Тогда
. Тогда
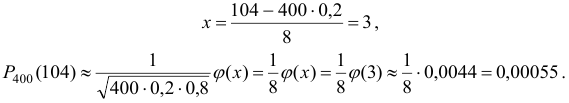
Значение функции 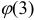 нашли по таблице.
нашли по таблице.
Интегральная теорема Лапласа
Теорема. Если вероятность 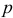 наступления события
наступления события 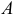 в каждом испытании постоянна и отлична от нуля и единицы, то вероятность
в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 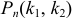 того, что событие
того, что событие 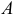 появится в
появится в 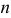 испытаниях от
испытаниях от 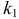 до
до 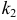 раз
раз 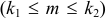 , приближенно равна определенному интегралу:
, приближенно равна определенному интегралу:
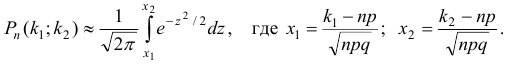
Интегральную теорему Лапласа иногда записывают в форме
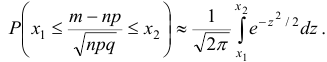
При решении используют таблицу для функции 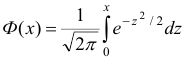 .
.
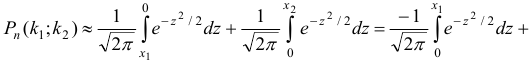
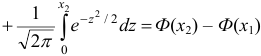 , где
, где 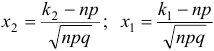 .
.
Функция 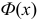 нечетная:
нечетная: 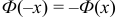 .
.
Пример №21
Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена:
а) не менее 70 и не более 80 раз; б) не более 70 раз.
Решение:
а) По условию 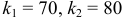 . Тогда
. Тогда
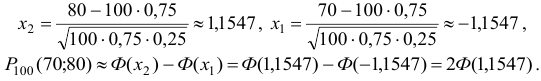
Значение функции Лапласа находим по таблице приложения 2. В таблице даны значения 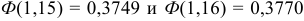 . В качестве ответа можно взять любое из этих значений или их среднеарифметическое:
. В качестве ответа можно взять любое из этих значений или их среднеарифметическое:
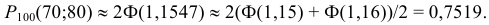
б) По условию 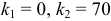 . Тогда
. Тогда
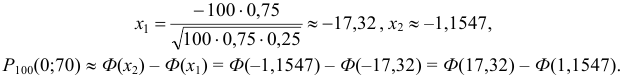
Значение функции Лапласа находим по таблице приложения 2:
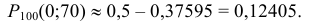
На этой странице размещён краткий курс лекций по теории вероятностей и математической статистике с теорией, формулами и примерами решения задач:
Теория вероятностей краткий курс для школьников и студентов
Возможно вам будут полезны эти страницы:

