Оглавление:
Наибольшее и наименьшее значение функции 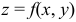
Функция, непрерывная в ограниченной замкнутой области 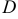 , достигает в ней наибольшего и наименьшего значения или в критических точках, или в точках, лежащих на границе области.
, достигает в ней наибольшего и наименьшего значения или в критических точках, или в точках, лежащих на границе области.
Для нахождения наибольшего и наименьшего значения функции в замкнутой ограниченной области 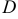 необходимо:
необходимо:
- Найти критические точки лежащие внутри данной области и вычислить в них значения функции;
- Найти наибольшее и наименьшее значения функции на границе области;
- Сравнить все полученные значения функции: самое большее (меньшее) и будет наибольшим (наименьшим) значением функции в данной области.
Как правило, граница области 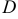 разбивается на ряд участков, каждый из которых определяется уравнением вида
разбивается на ряд участков, каждый из которых определяется уравнением вида 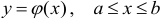 или
или 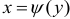 ,
, 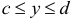 . Вдоль такого участка границы функция
. Вдоль такого участка границы функция 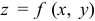 превращается в функцию только одной переменной
превращается в функцию только одной переменной 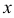 (или
(или 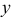 ). Иногда граница области
). Иногда граница области 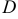 может задаваться параметрическими уравнениями:
может задаваться параметрическими уравнениями: 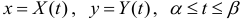 . В этом случае функция
. В этом случае функция 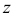 превращается вдоль границы в функцию параметра
превращается вдоль границы в функцию параметра 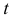 :
: 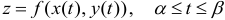 . Поэтому задача нахождения наибольшего и наименьшего значения функции
. Поэтому задача нахождения наибольшего и наименьшего значения функции 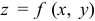 на границе области
на границе области 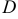 сводится к отысканию наибольшего и наименьшего значения функции одной переменной.
сводится к отысканию наибольшего и наименьшего значения функции одной переменной.
Пример №1
Найти наибольшее и наименьшее значения функции
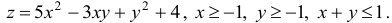
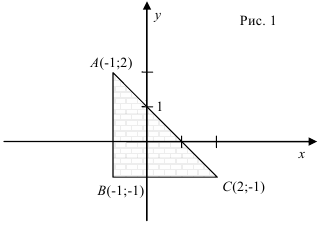
Решение:
Изобразим на координатной плоскости 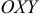 область
область 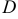 .
.
Область 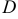 представляет собой треугольник
представляет собой треугольник 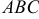 .
.
1) Найдем критические точки, лежащие внутри к 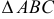 .
.
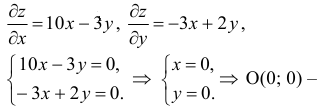
критическая точка, лежащая внутри 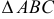 , причем
, причем 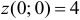 .
.
2) Исследуем теперь значения функции на контуре треугольника.
На стороне 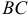 :
:
при 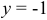 имеем
имеем 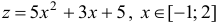 .
.
Найдем критические точки
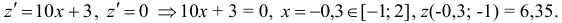
Найдем значения функции на концах отрезка 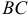 :
:
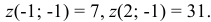
На стороне 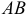 :
:
при 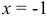 имеем
имеем 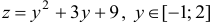 .
.
Найдем критические точки
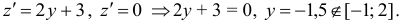
Найдем значения функции на концах отрезка 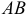 :
:
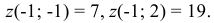
На стороне 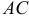 :
:
при 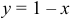 имеем
имеем 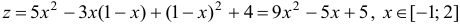 .
.
Найдем критические точки
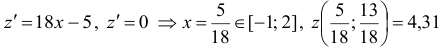
Значения функции на концах отрезка 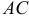 найдены ранее.
найдены ранее.
В итоге получим следующую таблицу возможных наибольших и наименьших значений функции.
Таблица 1

Из таблицы видно, что наибольшее значение 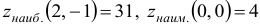 .
.
Пример №2
Найти наибольшее и наименьшее значения функции 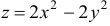 в круге
в круге 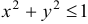 .
.
Решение:
Эту задачу можно решить аналогично первой задаче. Приведем второй способ решения. Окружность 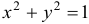 имеет следующие параметрические уравнения
имеет следующие параметрические уравнения 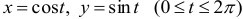 . Подставляя эти выражения для
. Подставляя эти выражения для 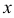 и
и 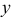 в формулу
в формулу 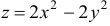 , получим функцию одной переменной
, получим функцию одной переменной 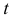 :
: 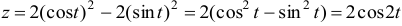 , т.е.
, т.е. 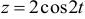 .
.
Находим критические точки: 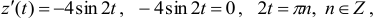
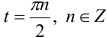 , но
, но 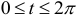 , следовательно,
, следовательно, 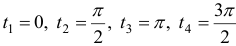 ,
, 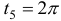 . Находим значения в критических точках и на концах отрезка
. Находим значения в критических точках и на концах отрезка 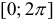 :
:
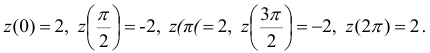
Следовательно, 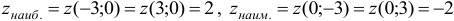 .
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Условный экстремум |
| Производная в данном направлении. Градиент функции |
| Метод наименьших квадратов |
| Двойной интеграл |

