Оглавление:
Задание: Нахождение производной сложной функции.
Цель: формирование умения находить производную сложной функции.
Задание для самостоятельной внеаудиторной работы:
13.1. Выучите, какую функцию называют сложной. Запомните правило дифференцирования сложной функции. Изучите технику нахождения производной сложной функции.
13.2. Найдите производную сложной функции:
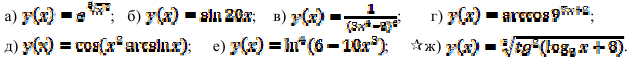
13.3. Найдите производную сложной функции в точке:
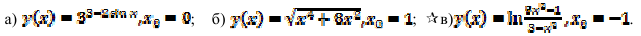
Методические указания по выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала:
Рассмотрим функции 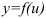 и
и 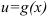 . Тогда функция
. Тогда функция 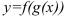 будет называться сложной функцией. Например, если
будет называться сложной функцией. Например, если 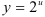 , а
, а 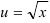 , то
, то 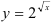 будет являться сложной функцией.
будет являться сложной функцией.
Для нахождения производной сложной функции используется следующая теорема, если функция 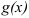 дифференцируема по переменной
дифференцируема по переменной 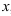 , а функция
, а функция 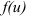 дифференцируема по переменной
дифференцируема по переменной 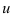 , то сложная функция
, то сложная функция 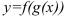 дифференцируема по переменной
дифференцируема по переменной 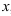 , причем её производная вычисляется по формуле:
, причем её производная вычисляется по формуле: 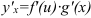 .
.
Функцию 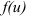 называют основной функцией, a
называют основной функцией, a 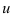 — «сложностью». Тогда правило нахождения производной сложной функции будет иметь вид: производная сложной функции равна производной основной функции, умноженной на производную «сложности»:
— «сложностью». Тогда правило нахождения производной сложной функции будет иметь вид: производная сложной функции равна производной основной функции, умноженной на производную «сложности»: 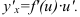
Для нахождения производных конкретных сложных функций целесообразно использовать следующую технику: принять какое-либо выражение за 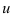 , чтобы прийти к одной из формул таблицы «Формулы дифференцирования сложных функций».
, чтобы прийти к одной из формул таблицы «Формулы дифференцирования сложных функций».
Формулы дифференцирования сложных функций

Рассмотрим нахождение производных сложных функций на конкретных примерах.
Пример 1.
Найдите производную функции 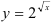 .
.
Решение:
Функция 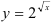 — сложная функция. Обозначим
— сложная функция. Обозначим 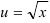 и придем к показательной функции
и придем к показательной функции 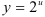 . Найдем ее производную по таблице производных сложных функций:
. Найдем ее производную по таблице производных сложных функций:
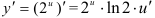 . Заменяя
. Заменяя 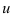 через
через 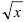 придем к производной вида:
придем к производной вида:
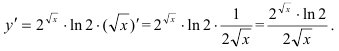
Ответ: 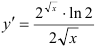 .
.
Пример 2.
Найдите производную функции 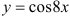 .
.
Решение:
Функция 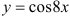 — сложная функция. Обозначим
— сложная функция. Обозначим 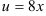 и придем к тригонометрической функции
и придем к тригонометрической функции 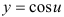 . Найдем ее производную по таблице производных сложных функций:
. Найдем ее производную по таблице производных сложных функций:

Ответ: 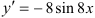 .
.
Пример 3.
Найдите производную функции 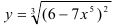 в точке
в точке 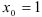 .
.
Решение:
Сначала продифференцируем данную функцию. Функция 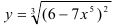 — сложная функция. Представим исходную функцию в виде степени:
— сложная функция. Представим исходную функцию в виде степени: 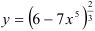 . Обозначим
. Обозначим 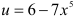 и придем к степенной функции вида
и придем к степенной функции вида 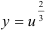 . Найдем ее производную по таблице производных сложных функций:
. Найдем ее производную по таблице производных сложных функций: 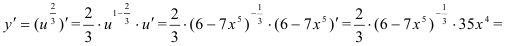
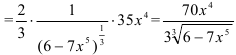 . Итак,
. Итак, 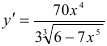 .
.
Затем в найденную производную 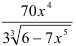 вместо аргумента подставим
вместо аргумента подставим 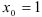 . Получим:
. Получим: 
Ответ: 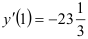 .
.
Пример 4.
Найдите производную функции 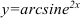 .
.
Решение:
Функция 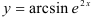 — сложная функция. Обозначим
— сложная функция. Обозначим 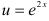 и придем к обратной тригонометрической функции
и придем к обратной тригонометрической функции 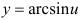 . Найдем ее производную по таблице производных сложных функций:
. Найдем ее производную по таблице производных сложных функций: 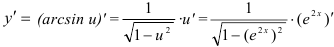 .
.
Однако, мы видим, что 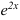 тоже сложная функция. Обозначив
тоже сложная функция. Обозначив 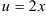
и придя к показательной функции 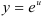 , найдем её производную по таблице производных сложных функций:
, найдем её производную по таблице производных сложных функций: 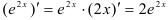 (здесь мы применили краткую запись решения).
(здесь мы применили краткую запись решения).
Получили, что 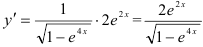 .
.
Ответ: 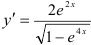 .
.

