Пример решённой на заказ задачи №130.
Найти наибольшую кривизну параболы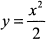 
.
Решение:
Находим производные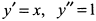 
. Подставляя найденные значения в формулу (1), получим 
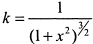. Кривизна будет наибольшей, когда знаменатель будет наименьшим, т. е. при 
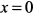. Таким образом, наибольшая кривизна равна 
.
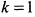На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №126. |
| Пример решённой на заказ задачи №128. |
| Пример решённой на заказ задачи №132. |
| Пример решённой на заказ задачи №134. |
