Пример решённой на заказ задачи №93.
В данный шар вписать конус с наибольшим объемом.
Решение:
Объем конуса, вписанного в шар (рис. 7.33), равен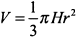 
, где 
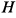— высота конуса, 
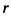— радиус основания.
Обозначим за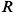 
— радиус шара, тогда из 
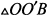имеем: 
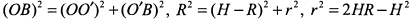. Отсюда 
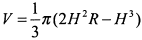. Принимая объем конуса за функцию, наибольшую его величину находим, исследуя эту функцию на экстремум: 
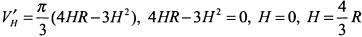. При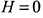 
функция, естественно, не может иметь наибольшего объема. При 
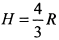производная 
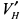меняет знак с плюса на минус, т. е. функция имеет максимум. Следовательно, наибольший объем конуса, вписанного в шар, при высоте конуса 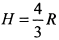, где радиус шара 
.
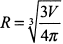На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №89. |
| Пример решённой на заказ задачи №91. |
| Пример решённой на заказ задачи №95. |
| Пример решённой на заказ задачи №97. |
