Уравнения первого порядка с разделяющимися переменными
Уравнение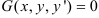 
называется дифференциальным уравнением первого порядка с разделяющимися переменными, если, после преобразований, его можно привести к виду
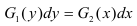
Такие уравнения решаются обычным интегрированием левой и правой частей. Пример:
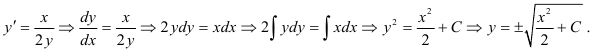
Таким образом, уравнение свелось к вычислению обычного неопределенного интеграла. Единственным, не слишком существенным отличием, является то, что постоянная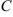 
может входить в алгебраические операции как составная часть. Полученное решение, содержащее произвольную постоянную, будет общим решением (общим интегралом) данного уравнения. Рассмотрим, как выглядят частные решения, если поставлены какие-либо дополнительные условия.
1. Пусть известно значение функции в точке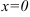 
(начальное условие), например, 
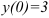. Подставим в общее решение:
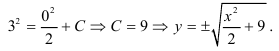
2. Пусть известно значение функции в точке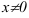 
(граничное условие), например, 
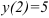. Подставим в общее решение:
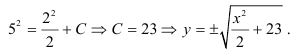
Результат, в котором определено конкретное значение константы 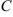с помощью начального или граничного условия и будет частным решением (частным интегралом) дифференциального уравнения.
Остальные темы находится на этой странице и там же можно заказать любые работы по высшей математике:
Обратите внимание на эти страниц, возможно они вам будут полезны:
| Теорема о среднем определенного интеграла |
| Применение определенного интеграла к вычислению площадей |
| Систематическое интегрирование |
| Изгибы функции и их определение |
