Применение определенного интеграла к вычислению площадей
Геометрический смысл определенного интеграла как площади криволинейной трапеции дает возможность применить его к вычислению любых площадей. Однако определенный интеграл в интервале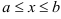 
далеко не всегда дает значение площади как физической величины, измеряемой в квадратных единицах. Необходимо учесть, что геометрический смысл построен на формальном приписывании знаков: части функции над осью 
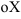(и площадь под ними) принимаются со знаком «плюс», а части функции под осью 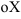(и площадь над ними) берутся со знаком «минус». Очевидно, что если поставить задачу о вычислении собственно площадей, то обязательно следует учесть строгую положительность понятия площади как физической величины. Чтобы полностью разобраться с разницей между геометрическим смыслом интеграла и площадью, рассмотрим пример: вычислить интеграл 
и площадь, которую ограничивает подынтегральная функция.
Нарисуем эскиз расчетной области и проведем вычисления по пунктам:
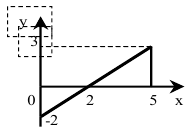
1. Вычислим интеграл: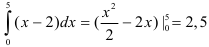 
.
2. По геометрическому смыслу интеграл является алгебраической суммой площадей нижнего и верхнего треугольников, т.е.
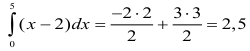
Как и следовало ожидать, результаты совпали. Подсчитаем площадь.
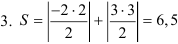квадратных единиц.
Здесь знак модуля обеспечивает безусловную положительность результатов и соответствие физическому смыслу. Таким образом, общая формула для вычисления площади с применением определенного интеграла будет иметь вид
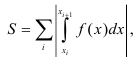
где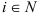 
— число подинтервалов, на которые разбивается площадь под кривой 
; 
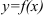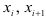— абсциссы начала и конца подинтервала.
Определение площади следует производить в два этапа. На первом решается уравнение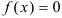 
и находится число подинтервалов. На втором этапе применяется формула площади. Рекомендуется выполнить эскиз расчетной области. В трудных случаях можно использовать графическое разложение сложной фигуры на сумму более простых.
Остальные темы находится на этой странице и там же можно заказать любые работы по высшей математике:
Обратите внимание на эти страниц, возможно они вам будут полезны:
| Формула трапеций |
| Теорема о среднем определенного интеграла |
| Уравнения первого порядка с разделяющимися переменными |
| Систематическое интегрирование |
