Пример решения заказа контрольной работы №52.
Найдите промежутки монотонности и экстремумы функции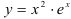 
.
Решение:
1. Данная функция определена на множестве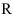 
.
Найдем первую производную функции по правилу производной произведения:
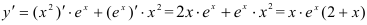
Определим критические точки первого рода
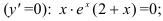
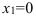или 
(
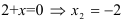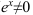для всех 
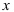из множества ).
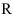На числовой оси отметим критические точк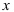и =-2 и 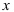=0. Эти точки разбивают область определения функции на три интервала 
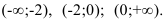Расставим знаки производной функции 
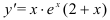на каждом из полученных интервалов:
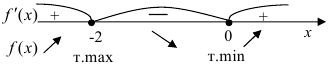
Согласно критерию возрастания и убывания функция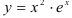 
возрастает при 
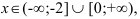, убывает при 
.
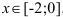Согласно критерию нахождения точек экстремума 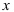=-2 — точка максимума, 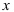=0 — точка минимума. Для нахождения экстремумов вычислим значения функции в этих точках:
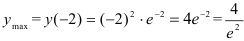— максимум функции;
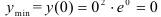— минимум функции.
Ответ: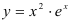 
возрастает при 
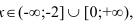, убывает при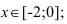 
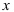=-2 — точка максимума;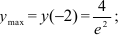 
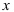= 5 — точка минимума;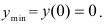 
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
| Пример решения заказа контрольной работы №49. |
| Пример решения заказа контрольной работы №50. |
| Пример решения заказа контрольной работы №54. |
| Пример решения заказа контрольной работы №56. |
