Для связи в whatsapp +905441085890

Метод касательных

Метод касательных

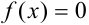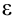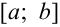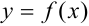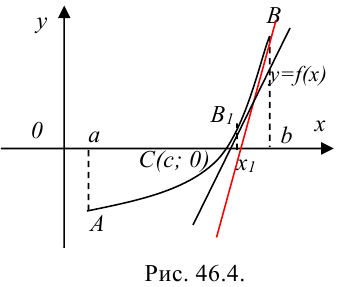
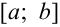Перед нами стоит все та же задача: найти корень уравнения вида Метод касательных с точностью Метод касательных, если известно, что корень принадлежит промежутку Метод касательных. Как и в предыдущем пункте введем функцию Метод касательных на отрезке Метод касательных (рис. 46.4), график которой пересекает ось 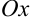Метод касательных в некоторой точке 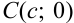Метод касательных. 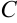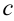Цель метода не изменилась — найти абсциссу точки Метод касательных — значение Метод касательных.

Выполним следующие действия:

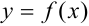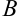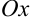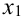  1. Проведем касательную к графику функции Метод касательныхв точке Метод касательных. Она пересекает ось Метод касательных в точке с абсциссой Метод касательных.
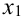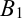  2. Выберем точку на кривой, абсцисса которой равна Метод касательных — точка Метод касательных.
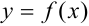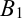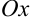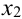  3. Проведем касательную к графику функции Метод касательных в точке Метод касательных. Она пересекает ось Метод касательных в точке с абсциссой Метод касательных.
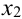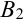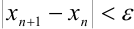  4. Выберем точку на кривой, абсцисса которой равна Метод касательных — точка Метод касательных и т.д. до тех пор, пока не будет справедливо неравенство: Метод касательных.

Выведем формулы для нахождения 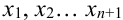Метод касательных:

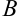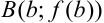
1. Выпишем координаты точки Метод касательных: Метод касательных

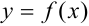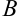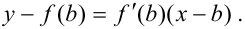
2. Составим уравнение касательной, проведенной к графику функции Метод касательных в точке Метод касательных: Метод касательных

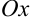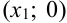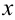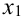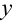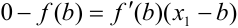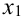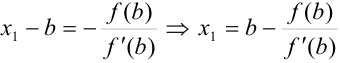3. Найдем точку пересечения касательной с осью Метод касательных. Она имеет координаты Метод касательных. Заменим в уравнении пункта 2 Метод касательных на Метод касательных, Метод касательных на 0: Метод касательных.

Выразим Метод касательных : Метод касательных.

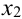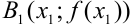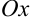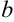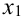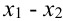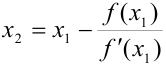4. Поскольку для нахождения Метод касательных нужно проводить новую касательную в точке Метод касательных и находить точку ее пересечения с осью Метод касательных, произведем по аналогии следующую замену: роль Метод касательных будет выполнять Метод касательных, роль Метод касательных. Получим, что Метод касательных.

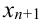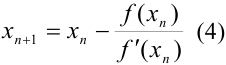5. Обобщим проведенные рассуждения. Для нахождения Метод касательных будем использовать следующую формулу: Метод касательных.

Метод касательных

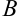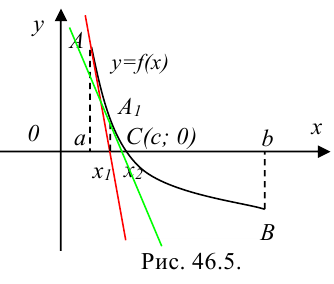
В рассмотренном нами случае исходной точкой, в которой проводилась первая касательная, была точка Метод касательных.

Возможен и другой вариант: исходной может быть точка 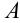Метод касательных (рис. 46.5).

Правило выбора исходной точки:

Исходной точкой является тот конец отрезка 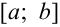Метод касательных, для которого знак функции совпадает со знаком второй производной в данной точке.

Пример №46.3.

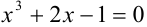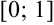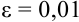Найти приближенное решение уравнения Метод касательных на Метод касательных, использую метод касательных с точностью Метод касательных.

Решение:

Составим функцию 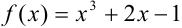Метод касательных.

1. Выберем исходную точку. Воспользуемся решением примера 46.2, где было показано, что для 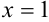Метод касательных знак функции совпадает со знаком второй производной. Следовательно, точка 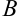Метод касательных будет являться исходной, а 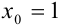Метод касательных — абсцисса исходной точки.

2. В силу достаточной сложности вычислений при применении данного метода, выполним расчеты в программе Microsoft Excel.

В качестве шапки таблицы возможен следующий вариант:

Метод касательных

В столбце 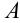Метод касательных будет указываться номер выполняемого шага 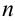Метод касательных. Первое значение 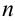Метод касательных выберем равным 0.

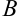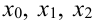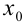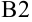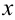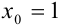В столбце Метод касательных будут располагаться значения Метод касательных и т.д. В качестве Метод касательных в ячейку Метод касательных заносится координата Метод касательных исходной точки. В нашем примере это Метод касательных.

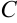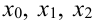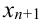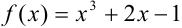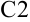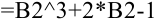В столбце Метод касательных будут содержаться значения функции в точках Метод касательных и т.д., необходимые для расчета Метод касательных по формуле (4). Поскольку Метод касательных, то в ячейку Метод касательных введем формулу: Метод касательных.

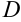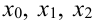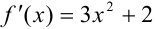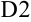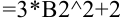В столбце Метод касательных будут содержаться значения производной функции в точках Метод касательных и т.д., необходимые для расчета по формуле (4). Поскольку Метод касательных, то в ячейку Метод касательных введем формулу: Метод касательных.

В столбце 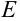Метод касательных будет осуществляться проверка того, не превосходит ли 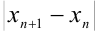Метод касательных заданной точности 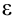Метод касательных. Эта проверка будет начинаться с первого шага, и ячейка 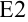Метод касательных не заполняется. После заполнения второй строки таблица будет иметь вид:

Метод касательных

Начнем заполнение третьей строки. Номер шага в ячейке 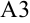Метод касательных будет равен 1.

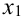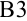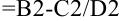Для расчета Метод касательных в ячейке Метод касательных применим формулу (4), которая в программе Microsoft Excel примет вид: Метод касательных.

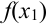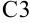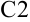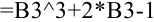Для расчета Метод касательных в ячейке Метод касательных достаточно просто скопировать формулу из ячейки Метод касательных, и она будет иметь вид: Метод касательных.

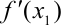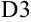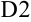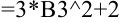Аналогично для расчета Метод касательных в ячейку Метод касательных достаточно скопировать формулу из ячейки Метод касательных, и она будет иметь вид: Метод касательных.

В ячейку 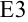Метод касательных занесем формулу для расчета модуля разности между последующим и предыдущим значением 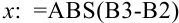Метод касательных. Произведем проверку: если содержимое этой ячейки больше 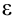Метод касательных, то расчеты необходимо продолжить, меньше — закончить.

После заполнения третьей строки таблица будет иметь вид:

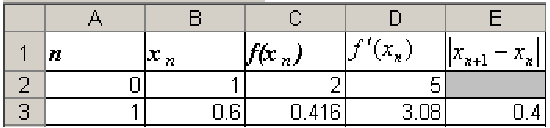
Метод касательных

Как отмечалось выше, все формулы уже введены, в дальнейшем будем использовать только автозаполнение и осуществлять проверку в столбце 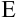Метод касательных. После выполнения следующих шагов таблица будет иметь вид:

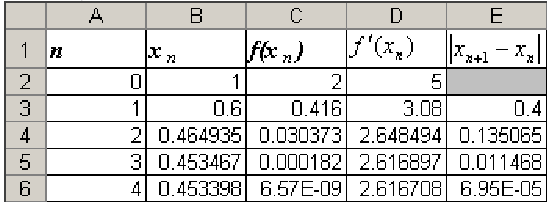
Метод касательных

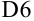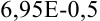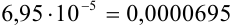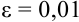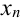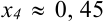Видим, что в ячейке Метод касательных содержимое Метод касательных (означает Метод касательных) стало меньше заданной точности Метод касательных, следовательно, расчеты следует закончить и в качестве приближенного решения уравнения взять последнее Метод касательных с точностью два знака после запятой. В нашем примере это Метод касательных.

Ответ: 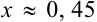Метод касательных.

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Понятие алгебраического и трансцендентного уравнения и методов их приближенного решения.
Метод хорд.
Задача численного интегрирования.
Формулы прямоугольников.