Рассмотрим правила проведения вычислений без строгого учета погрешностей, называемые правилами подсчета цифр.
- При сложении и вычитании приближенных чисел в результате сохраняют столько десятичных знаков, сколько их в наименее точном числе.
- При умножении и делении приближенных чисел в результате сохраняют столько значащих цифр, сколько их в числе с меньшим количеством значащих цифр.
- При возведении в степень и извлечении корня в результате сохраняют столько значащих цифр, сколько их в основании степени или подкоренном выражении.
- При выполнении промежуточных действий оставляют на один знак больше, чем требуют правила, а в результате запасной знак округляют.
- Если в вычислениях точность задана заранее, то вычисления ведут с запасным знаком, который в результате округляют.
- При вычислениях с использованием вычислительных средств допускается производить точные промежуточные вычисления, но результат должен быть записан с учетом правил 1-3.
Пример №45.6.
Произвести действия с приближенными числами:
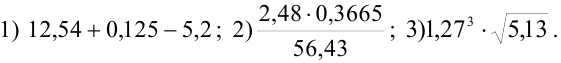
Решение:
1. Округляем все числа по наименее точному числу (числу 5,2 — 1 знак после запятой), оставляя запасной знак, и производим сложение:
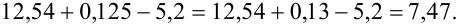
Запасной знак округляем и получаем ответ: 7,5.
2. Для умножения и деления чисел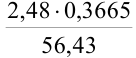 
найдем число с наименьшим количеством значащих цифр — 2,48 (3 значащие цифры). Округляем остальные числа до трех значащих цифр: 
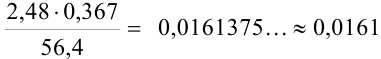. Результат также необходимо округлить до трех значащих цифр.
3. При возведении в степень и извлечении корня воспользуемся правилом 3.
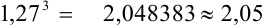(оставляем три значащие цифры как в основании степени).
Аналогично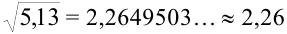 
.
Перемножим эти числа, оставляя в ответе 3 значащие цифры: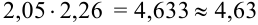 
.
Ответ: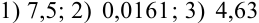 
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Относительная погрешность. |
| Запись приближенных чисел. Верные и значащие цифры. |
| Понятие алгебраического и трансцендентного уравнения и методов их приближенного решения. |
| Метод хорд. |
