Оглавление:
Над комплексными числами в показательной форме выполнимы те же операции и по тем же самым правилам, что и для чисел, заданных в тригонометрической форме. Покажем это.
Пусть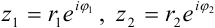 
. Над ними выполнимы следующие операции:
Умножение
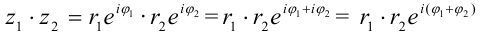
Получили что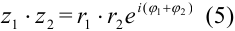 
. При умножении комплексных чисел в показательной форме их модули перемножаются, а аргументы складываются.
Деление
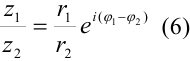. При делении комплексных чисел в показательной форме их модули делятся, а аргументы вычитаются.
Возведение в степень
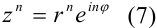. При возведении в степень комплексного числа в показательной форме модуль числа нужно возвести в 
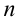-ю степень, а аргумент умножить на .
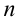Извлечение корня n-й степени
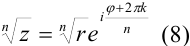, где 
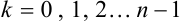принимает ровно 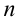значений.
Пример №43.4.
Для комплексных чисел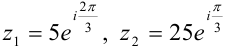 
найдите: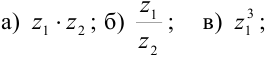 
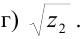
Решение:
а) Согласно формуле (5) получим
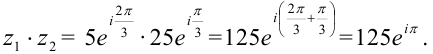
б) Используя формулу (6), находим
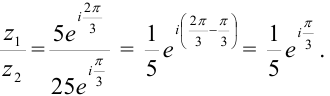
в) Применяя формулу (7), находим
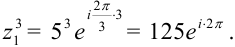
г) Извлечем квадратный корень из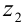 
по формуле (8): 
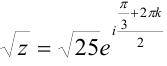, где параметр 
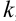будет принимать значения 0 и 1 (корней 2-й степени из числа существует ровно 2: 
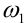и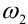 
).
При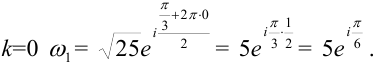 
При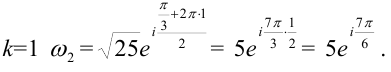 
Ответ: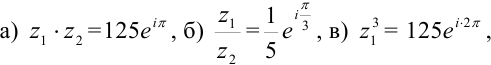 
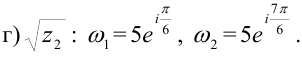
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
