Комплексное число 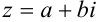 можно изобразить точкой на плоскости с координатами
можно изобразить точкой на плоскости с координатами 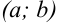 . Для этого выберем в плоскости прямоугольную декартову систему координат. Действительную часть
. Для этого выберем в плоскости прямоугольную декартову систему координат. Действительную часть 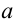 комплексного числа будем откладывать на оси
комплексного числа будем откладывать на оси 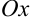 , коэффициент при мнимой части
, коэффициент при мнимой части 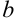 — на оси
— на оси 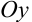 (рис. 42.2).
(рис. 42.2).
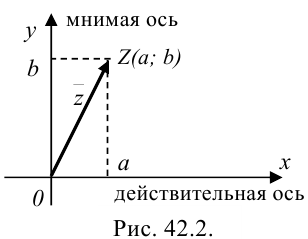
Каждой точке плоскости с координатами 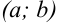 соответствует только один вектор с началом в точке
соответствует только один вектор с началом в точке 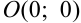 и концом в точке
и концом в точке 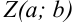 . Поэтому комплексное число
. Поэтому комплексное число 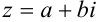 можно также изобразить в виде вектора
можно также изобразить в виде вектора 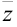 с началом в начале координат и концом в точке
с началом в начале координат и концом в точке 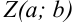 (рис. 42.2).
(рис. 42.2).
Плоскость, точкам которой сопоставлены комплексные числа, называется комплексной плоскостью.
Таким образом, геометрически комплексное число можно
представлять как
- точку на комплексной плоскости;
- вектор на комплексной плоскости.
Обе эти интерпретации допустимы, хотя вторая используется в математике чаще.
Действительные числа (как частный случай комплексных) изображаются точками, лежащими на оси 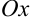 , а чисто мнимые комплексные числа изображаются точками, лежащими на оси
, а чисто мнимые комплексные числа изображаются точками, лежащими на оси 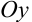 . В связи с этим ось
. В связи с этим ось 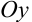 называется действительной осью, а ось
называется действительной осью, а ось 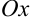 — мнимой осью комплексной плоскости.
— мнимой осью комплексной плоскости.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
