Оглавление:
В алгебраической форме над комплексными числами удобно выполнять следующие операции:
- сложение;
- вычитание;
- умножение;
- деление.
Сложение, вычитание и умножение комплексных чисел производят по правилам соответствующих действий над многочленами.
Пример №42.2.
Для комплексных чисел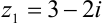 
и 
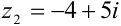найти:
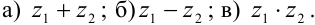
Решение:
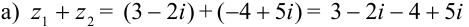
Действительную часть комплексного числа будем складывать с действительной частью, мнимую — с мнимой: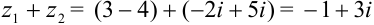 
.
При сложении двух комплексных чисел в алгебраической форме получили комплексное число также в алгебраической форме.
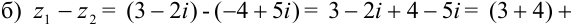
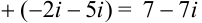— комплексное число в алгебраической форме.
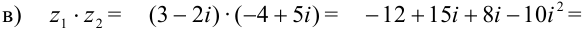
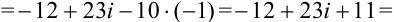
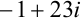— комплексное число в алгебраической форме.
Ответ:
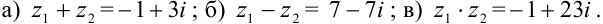
Для того чтобы ввести операцию деления для комплексных чисел, заданных в алгебраической форме, введем понятие сопряженных чисел.
Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью.
Например, числа 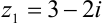и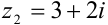 
— сопряженные, 
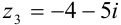и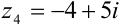 
— также сопряженные.
Найдем произведение любых двух сопряженных чисел, например 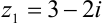и :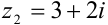
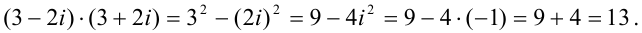
Видим, что произведение двух сопряженных комплексных чисел равно числу действительному. Это свойство сопряженных чисел используется для деления комплексных чисел в алгебраической форме.
Чтобы выполнить деление комплексных чисел в алгебраической форме, необходимо домножить числитель и знаменатель дроби на число, сопряженное знаменателю. Рассмотрим операцию деления комплексных чисел на конкретном примере:
Пример №42.3.
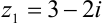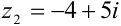Для комплексных чисел и найти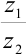 
.
Решение:
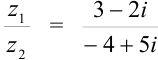. Домножим числитель и знаменатель дроби на число 
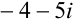, сопряженное знаменателю:
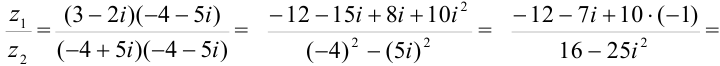
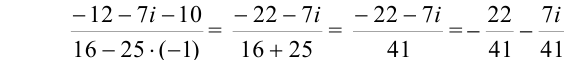
— комплексное число в алгебраической форме.
Ответ: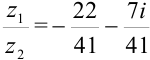 
.
Подчеркнем, что при сложении, вычитании, умножении и делении комплексных чисел в алгебраической форме в результате всегда получается комплексное число также в алгебраической форме.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие мнимой единицы. |
| Алгебраическая форма комплексного числа. |
| Решение квадратных уравнений с отрицательным дискриминантом. |
| Геометрическая интерпретация комплексных чисел. |
