Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид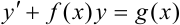 
, где 
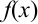и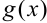 
— заданные функции, содержащие только переменную 
.
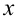Данное дифференциальное уравнение получило название «линейное» поскольку содержит функци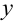и 
и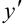 
в первой степени (линейное относительно 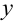и ).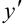
Например, уравнение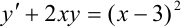 
будет являться линейным, поскольку имеет вид 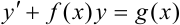, где 
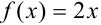, a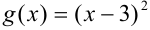 
.
Уравнение вида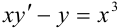 
легко приводится к линейному делением каждого слагаемого на 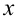(множитель перед ): 
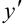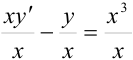или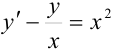 
. Полученное уравнение действительно является линейным, поскольку имеет вид 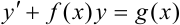, где 
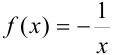, a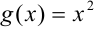 
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
