Однородное уравнение можно преобразовать к уравнению с разделяющимися переменными при помощи подстановки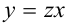 
, где 
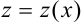— новая неизвестная функция.
Найдем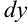 
по правилу нахождения производной произведения: 
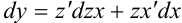или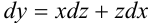 
.
Сформулируем алгоритм решения однородных дифференциальных уравнений:
- Выполнить подстановк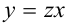и: и 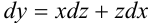. В получившемся дифференциальном уравнении раскрыть скобки и привести подобные слагаемые. Должно получиться уравнение с разделяющимися переменными.
- Проинтегрировать обе части уравнения с разделяющимися переменными относительно переменных
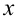и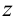 
. Найти общее решение дифференциального уравнения. - В общем решении вернуться к переменным 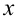и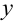
, подставив вместо 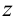выражение: 
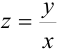. - Выписать в ответе получившееся общее решение дифференциального уравнения.
Пример №39.2.
Найдите решение дифференциального уравнения: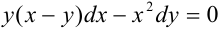 
.
Решение:
Данное уравнение — однородное дифференциальное уравнение первого порядка.
1. Выполним подстановк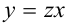и: и :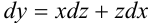
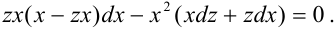
Раскроем скобки:
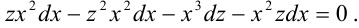
Приведем подобные слагаемые: первое и последнее взаимно уничтожаются. Получим:
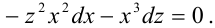
Перед нами уравнение с разделяющимися переменными. Соберем в левой части выражения, содержащие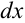 
, в правой — выражения, содержащие .
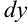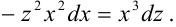
Тогда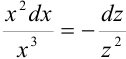 
или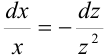 
— уравнение с разделенными переменными.
2. Интегрируя обе части, получим: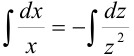 
или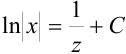 
.
3. Подставим вместо 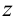выражение: 
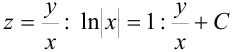или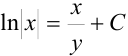 
. Это и есть общее решение исходного однородного дифференциального уравнения.
Ответ: .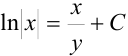
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
