Как и в случае ряда Тейлора (Маклорена), ряд Фурье не всегда сходится к порождающей функции. Выясним, при каких условиях ряд Фурье для функции  всё-таки сходится и имеет своей суммой как раз функцию
всё-таки сходится и имеет своей суммой как раз функцию  .
.
Эти условия изложены в теореме Дирихле, представляющей собой достаточное условие разложимости периодической функции  с периодом
с периодом 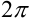 в ряд Фурье. Сформулируем её без доказательства.
в ряд Фурье. Сформулируем её без доказательства.
Теорема Дирихле: Пусть периодическая функция  с периодом
с периодом 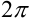 на отрезке
на отрезке 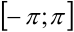 удовлетворяет двум условиям:
удовлетворяет двум условиям:
1)  кусочно — непрерывна, т.е. непрерывна или имеет конечное число точек разрыва первого рода;
кусочно — непрерывна, т.е. непрерывна или имеет конечное число точек разрыва первого рода;
2)  кусочно — монотонна, т.е. монотонна на всём отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна. Тогда соответствующий функции
кусочно — монотонна, т.е. монотонна на всём отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна. Тогда соответствующий функции  ряд Фурье сходится на этом отрезке и при этом:
ряд Фурье сходится на этом отрезке и при этом:
- в точках непрерывности функции сумма ряда совпадает с самой функцией:
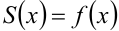 ;
; - в каждой точке разрыва
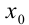 функции
функции  сумма ряда равна среднему арифметическому пределов функции в данной точке справа и слева;
сумма ряда равна среднему арифметическому пределов функции в данной точке справа и слева; - на концах отрезка (в точках
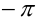 и
и 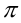 ) сумма ряда равна
) сумма ряда равна
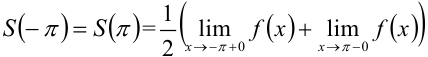
Таким образом, если функция  с периодом
с периодом 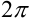 на отрезке
на отрезке 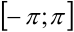 удовлетворяет условиям теоремы Дирихле, то для неё имеет место разложение в ряд Фурье:
удовлетворяет условиям теоремы Дирихле, то для неё имеет место разложение в ряд Фурье: 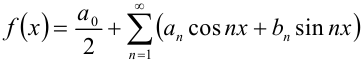 , где коэффициенты Фурье
, где коэффициенты Фурье
вычисляются по формулам
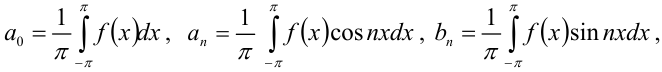
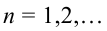
Заметим, что большинство функций, которые встречаются в математике и её приложениях, удовлетворяют условиям теоремы Дирихле, поэтому для них ряд Фурье сходится к порождающей функции в обычном смысле. Однако существуют функции, не удовлетворяющие условиям теоремы Дирихле, но при этом разложимые в ряд Фурье. Таким образом, теорема Дирихле даёт лишь достаточное условие разложимости, но не необходимое.
Пример №37.2.
Разложите в ряд Фурье функцию 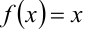 на отрезке
на отрезке 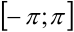 .
.
Решение:
Так как функция 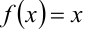 дифференцируема на
дифференцируема на 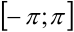 и удовлетворяет условиям теоремы Дирихле, то она разложима в ряд Фурье. Собственно ряд Фурье для неё на
и удовлетворяет условиям теоремы Дирихле, то она разложима в ряд Фурье. Собственно ряд Фурье для неё на 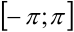 был получен в примере 37.1.:
был получен в примере 37.1.:
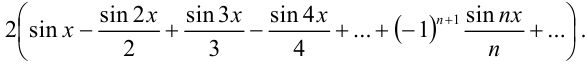
Следовательно, разложение в ряд Фурье для функции 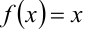 на отрезке
на отрезке 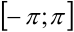 имеет вид:
имеет вид:
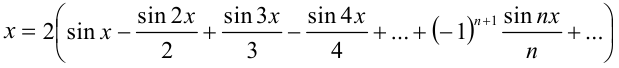
При этом значение полученного ряда в концах интервала равно 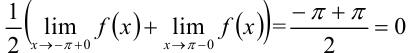 , следовательно, сумма ряда равна значению порождающей функции
, следовательно, сумма ряда равна значению порождающей функции 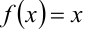 для всех точек интервала
для всех точек интервала 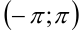 .
.
Ответ: 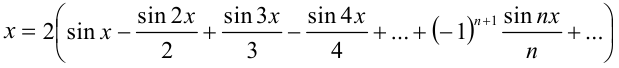 .
.

