Оглавление:
Формально ряд Тейлора (Маклорена) можно построить для любой бесконечно дифференцируемой функции  в окрестности точки
в окрестности точки 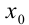 . Но отсюда ещё не следует, что он будет сходиться к данной функции
. Но отсюда ещё не следует, что он будет сходиться к данной функции  . Он может оказаться расходящимся или сходиться, но не к функции
. Он может оказаться расходящимся или сходиться, но не к функции  . Так, например, функция
. Так, например, функция 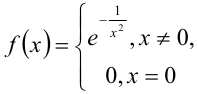 имеет в точке
имеет в точке 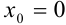 производные всех порядков, причём
производные всех порядков, причём 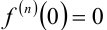 при всяком
при всяком 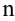 . Ряд Маклорена для
. Ряд Маклорена для
неё имеет вид 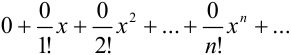 Он сходится, но его сумма
Он сходится, но его сумма 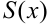 в любой точке
в любой точке  равна нулю, а не
равна нулю, а не 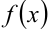 .
.
Условия, при которых ряд Тейлора (Маклорена) сходится к порождающей функции, изложены в теореме. Сформулируем её без доказательства.
Теорема: Если все производные функции  ограничены в некоторой окрестности точки
ограничены в некоторой окрестности точки 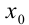 (
(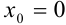 ) одним и тем же числом, то для любого
) одним и тем же числом, то для любого  из этой окрестности ряд Тейлора (Маклорена) для функции
из этой окрестности ряд Тейлора (Маклорена) для функции  сходится к данной функции, т.е. имеет место разложение
сходится к данной функции, т.е. имеет место разложение
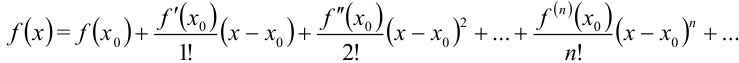
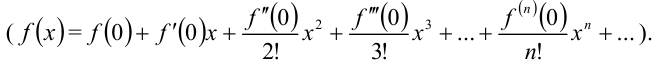
Для разложения некоторой функции  в ряд Тейлора (Маклорена) удобно использовать следующий алгоритм:
в ряд Тейлора (Маклорена) удобно использовать следующий алгоритм:
1) вычислить значения функции и всех её производных при 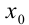 (
(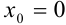 );
);
2) составить ряд Тейлора (Маклорена) для функции  ;
;
3) проверить выполнение условий теоремы о разложении функции в ряд (доказать, что все производные функции ограничены в некоторой окрестности точки 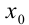 (
(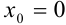 ) одним и тем же числом);
) одним и тем же числом);
4) записать разложение функции  в ряд Тейлора (Маклорена).
в ряд Тейлора (Маклорена).
Рассматривая разложение в ряд Тейлора некоторых элементарных функций, ограничимся рядами Маклорена, которые чаще всего используются на практике.
Пример №36.3.
Разложите функцию 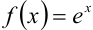 в ряд Маклорена.
в ряд Маклорена.
Решение:
Для разложения функции 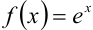 в ряд Маклорена воспользуемся алгоритмом: 1) значения функции
в ряд Маклорена воспользуемся алгоритмом: 1) значения функции 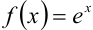 и её производных вычислены в примере 36.2.:
и её производных вычислены в примере 36.2.:
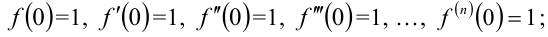
2) ряд Маклорена для функции 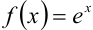 составлен в примере 36.2.:
составлен в примере 36.2.:
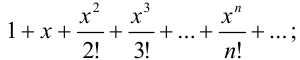
3) проверим выполнение условий теоремы о разложении функции в ряд: для данного  найдём интервал
найдём интервал 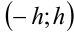 , содержащий число
, содержащий число  , и обозначим
, и обозначим 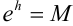 . Тогда для любой производной функции имеем
. Тогда для любой производной функции имеем 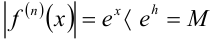 . Таким образом, все производные функции
. Таким образом, все производные функции 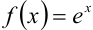 в некоторой окрестности
в некоторой окрестности 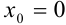 ограничены одним и тем же числом
ограничены одним и тем же числом 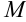 . Значит, условия теоремы выполнены, и функция может быть разложена в ряд.
. Значит, условия теоремы выполнены, и функция может быть разложена в ряд.
4) запишем разложение функции 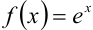 в ряд Маклорена:
в ряд Маклорена:
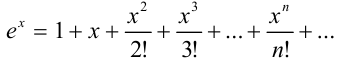
Ответ: 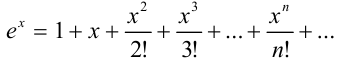
Аналогичным образом можно получить разложения в ряд Маклорена следующих элементарных функций, которые рекомендуется запомнить:
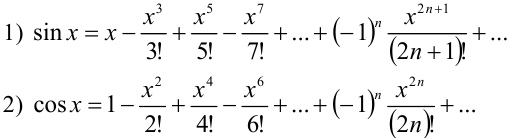
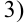 биномиальный ряд:
биномиальный ряд:
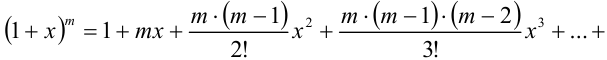
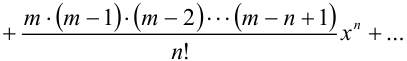
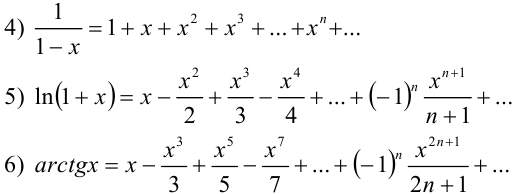
Разложение некоторых функций в ряд Маклорена можно получить, выполняя те или иные преобразования над уже имеющимися разложениями. К таким преобразованиям относятся замена переменной, сложение, вычитание, умножение, дифференцирование и интегрирование степенных рядов.
Обратимся к примерам получения подобных разложений.
Пример №36.4.
Используя известные разложения, разложите в ряд Маклорена функцию 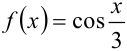 .
.
Решение:
Воспользуемся известным разложением в ряд функции 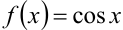 :
:
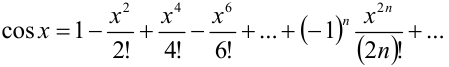
Заменим в данном разложении  на
на 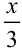 , получим:
, получим:
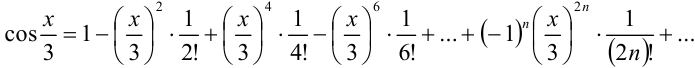
Таким образом,
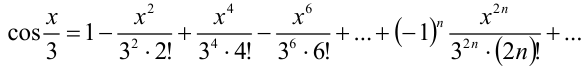
Ответ: 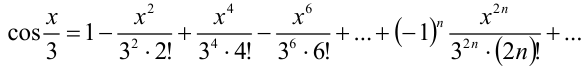
Пример №36.5.
Разложите в ряд Маклорена функцию 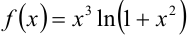 .
.
Решение:
Функция 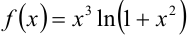 представляет собой произведение
представляет собой произведение 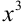 на
на 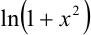 , поэтому для её разложения в ряд Маклорена воспользуемся разложением функции
, поэтому для её разложения в ряд Маклорена воспользуемся разложением функции 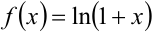 :
:
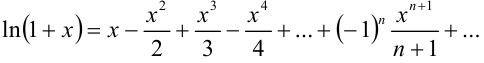
Заменим в этом разложении  на
на 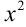 , получим:
, получим:
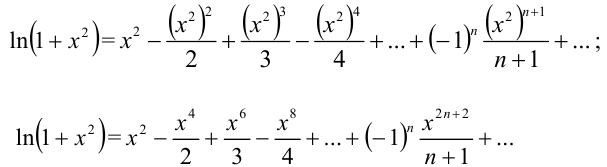
Умножим разложение 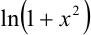 на
на 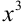 :
:
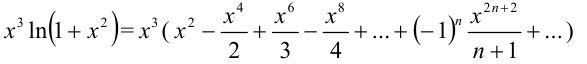
Таким образом, 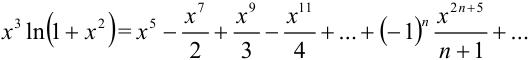
Ответ: 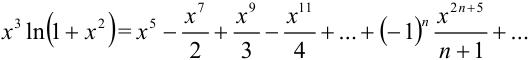
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Свойства степенных рядов. |
| Ряды Тейлора и Маклорена. |
| Практическое применение разложений функций в ряд. |
| Тригонометрический ряд Фурье. |

