Множество всех точек сходимости степенного ряда 
называется его областью сходимости. Поскольку степенной ряд всегда сходится при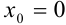 
, то его область сходимости содержит по крайней мере одну точку (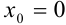). Область сходимости степенного ряда состоит из одной точки (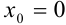), если радиус его сходимости равен нулю (
).
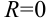Если радиус сходимости степенного ряда равен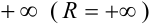 
, то область его сходимости будет совпадать с интервалом сходимости 
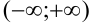. Так, для ряда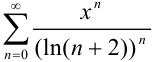 
рассмотренного в примере 35.3., областью сходимости является .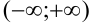
Если радиус сходимости степенного ряда отличен от нуля и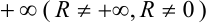 
, то область сходимости данного ряда либо совпадает с его интервалом сходимости, либо получается из этого интервала добавлением одной или обеих граничных точек. Это решается дополнительным исследованием сходимости степенного ряда на концах интервала сходимости.
Пример №35.4.
Найдите область сходимости степенного ряда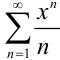 
.
Решение:
Выясним, чему равен радиус сходимости данного степенного ряда. Искать его будем по формул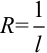е: 
, где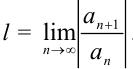 
. Для этого:
1. найдём коэффициент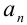 
: 
;
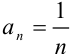2. найдём коэффициент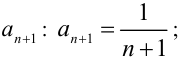 
3. найдём отношение коэффициентов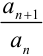 
:
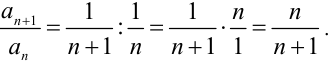
Таким образом, получим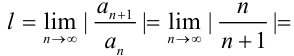 
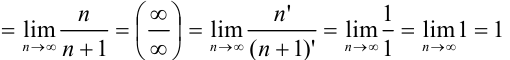(при
раскрытии неопределённости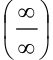 
использовали правило Лопиталя). Следовательно, так как 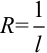, а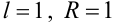 
.
Радиус сходимости степенного ряда (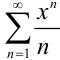
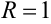) отличен от нуля и 
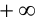, значит, область его сходимости либо совпадает с интервалом сходимости, либо получается из него добавлением одной или обеих граничных точек.
Найдём интервал сходимости степенного ряда по формуле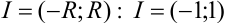 
.
Исследуем сходимость степенного ряда 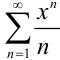на концах интервала сходимости. При 
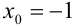получаем условно сходящийся знакочередующийся ряд 
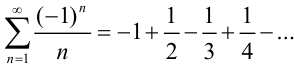(пример 34.4. лекции 34). Значит, 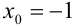— точка сходимости ряда 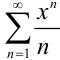. При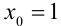 
получаем расходящийся гармонический ряд 
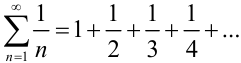(лекция 32). Значит, 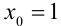— точка расходимости ряда 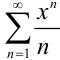. Следовательно, областью сходимости степенного ряда 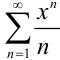будет [-1;1) .
Ответ: [-1;1).
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие функционального ряда. |
| Понятие степенного ряда. Радиус и интервал сходимости. |
| Свойства степенных рядов. |
| Ряды Тейлора и Маклорена. |
