Оглавление:
Среди функциональных рядов в математике и её приложениях особое значение имеет степенной ряд.
Функциональный ряд вида 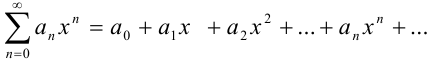 , членами которого являются степенные функции аргумента
, членами которого являются степенные функции аргумента  , называется степенным.
, называется степенным.
Действительные числа 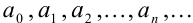 называют коэффициентами степенного ряда (
называют коэффициентами степенного ряда ( — действительная переменная).
— действительная переменная).
По определению, степенными рядами являются следующие функциональные ряды
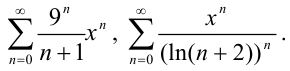
Рассматривают также степенной ряд в точке 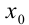 — степенной ряд вида
— степенной ряд вида 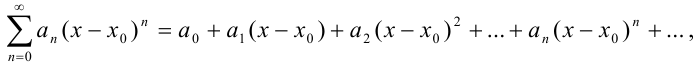 где
где 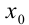 — фиксированное число. Если произвести замену
— фиксированное число. Если произвести замену 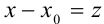 , то степенной ряд в точке
, то степенной ряд в точке 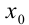 примет вид
примет вид 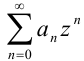 . Поэтому при изучении степенных рядов можно ограничиться степенными рядами вида
. Поэтому при изучении степенных рядов можно ограничиться степенными рядами вида  .
.
У степенного ряда  счет членов ведется, как правило, не с единицы, а с нуля: первый член называется нулевым, второй — первым и т.д. Для степенного ряда такой счет является естественным, так как нулевой член представляет собой произведение коэффициента
счет членов ведется, как правило, не с единицы, а с нуля: первый член называется нулевым, второй — первым и т.д. Для степенного ряда такой счет является естественным, так как нулевой член представляет собой произведение коэффициента 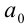 на нулевую степень переменной
на нулевую степень переменной  :
: 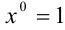 ; первый член — произведение коэффициента
; первый член — произведение коэффициента 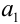 на первую степень переменной
на первую степень переменной  :
: 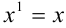 и, вообще,
и, вообще, 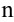 -й член равен произведению коэффициента
-й член равен произведению коэффициента 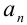 на
на 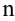 -ую степень переменой
-ую степень переменой  :
: 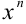 .
.
Любой степенной ряд  всегда сходится в точке
всегда сходится в точке 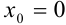 . Действительно, если подставим в ряд
. Действительно, если подставим в ряд  вместо
вместо 
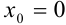 , получим числовой ряд
, получим числовой ряд 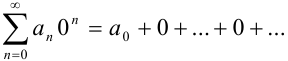 , сумма которого равна
, сумма которого равна 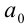 . По определению, данный числовой ряд сходится. Таким образом,
. По определению, данный числовой ряд сходится. Таким образом, 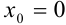 всегда является точкой сходимости степенного ряда
всегда является точкой сходимости степенного ряда  . Возникает вопрос: есть ли у степенного ряда
. Возникает вопрос: есть ли у степенного ряда  другие точки сходимости?
другие точки сходимости?
Ответ на него дает теорема Н.Абеля (1802-1829) — выдающегося норвежского математика, и следствие из неё. Рассмотрим их без доказательства.
Теорема Абеля: Если степенной ряд  сходится в точке
сходится в точке 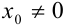 , то он сходится, и притом абсолютно, для всех
, то он сходится, и притом абсолютно, для всех  , удовлетворяющих неравенству:
, удовлетворяющих неравенству: 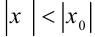 .
.
Следствие: Если степенной ряд  расходится в точке
расходится в точке 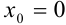 , то он расходится для всех
, то он расходится для всех  , удовлетворяющих неравенству:
, удовлетворяющих неравенству: 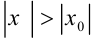 .
.
Из теоремы Абеля и следствия из неё следует (рис. 35.1.), что если 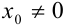 — точка сходимости степенного ряда
— точка сходимости степенного ряда  , то интервал
, то интервал 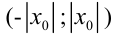 весь состоит из точек сходимости данного ряда; при всех значениях
весь состоит из точек сходимости данного ряда; при всех значениях  вне этого интервала степенной ряд расходится.
вне этого интервала степенной ряд расходится.
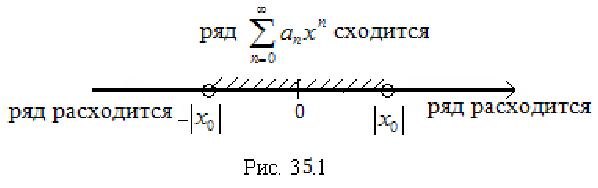
Радиусом сходимости 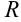 степенного ряда
степенного ряда  называется неотрицательное действительное число или
называется неотрицательное действительное число или 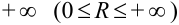 , удовлетворяющее условиям: при всех
, удовлетворяющее условиям: при всех  , для которых
, для которых 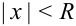 степенной ряд
степенной ряд  сходится; при всех
сходится; при всех  , для которых
, для которых 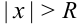 , степенной ряд
, степенной ряд  расходится.
расходится.
Если степенной ряд  сходится лишь в одной точке
сходится лишь в одной точке 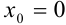 , то его радиус сходимости равен 0:
, то его радиус сходимости равен 0: 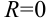 .
.
Если степенной ряд  сходится при всех действительных значениях переменной
сходится при всех действительных значениях переменной  (во всех точках числовой оси), то его радиус сходимости равен
(во всех точках числовой оси), то его радиус сходимости равен 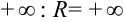 .
.
Таким образом, у любого степенного ряда сеть радиус сходимости.
Найти радиус сходимости степенного ряда позволяет следующая теорема, которую приведем без доказательства.
Теорема. Если для степенного ряда  существуют конечные или бесконечные пределы
существуют конечные или бесконечные пределы 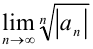 или
или 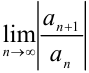 , равные
, равные 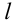 , то радиус сходимости степенного ряда находится по формуле:
, то радиус сходимости степенного ряда находится по формуле: 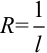 .
.
Замечание: Если для степенного ряда 
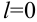 , то его радиус сходимости
, то его радиус сходимости 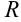 равен
равен 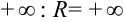 ;
; 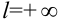 , то его радиус сходимости
, то его радиус сходимости 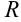 равен 0:
равен 0: 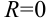 .
.
Обратимся к примерам нахождения радиуса сходимости степенного ряда.
Пример №35.2.
Найдите радиус сходимости степенного ряда 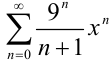 .
.
Решение:
Радиус сходимости степенного ряда 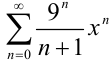 будем искать по формуле:
будем искать по формуле: 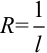 , где
, где 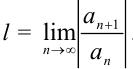 . Для этого:
. Для этого:
1. найдем коэффициент 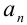 :
: 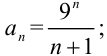
2. найдем коэффициент 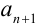 :
: 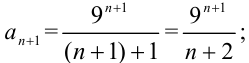
3. найдем отношение коэффициентов 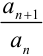 :
: 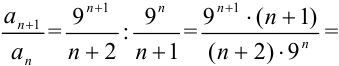
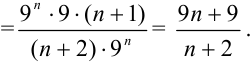
Таким образом, получим
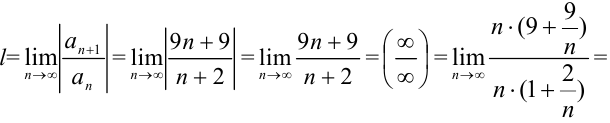
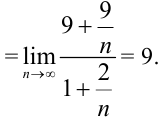
Следовательно, так как 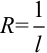 , а
, а 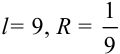 .
.
Ответ: 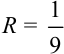 .
.
Пример №35.3.
Найдите радиус сходимости степенного ряда 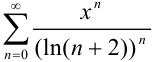 .
.
Решение:
Радиус сходимости степенного ряда 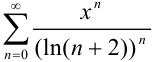 будем искать по формуле:
будем искать по формуле: 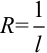 , где
, где 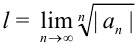 . Для этого:
. Для этого:
1. найдём коэффициент 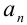 :
: 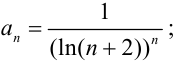
2. найдем 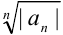 :
: 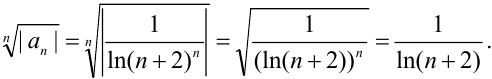
Таким образом, получим 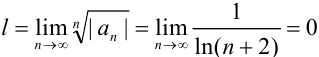 .
.
Следовательно, по замечанию, если 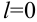 , то
, то 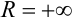 .
.
Ответ: 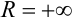 .
.
Если 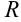 — радиус сходимости степенного ряда
— радиус сходимости степенного ряда  , то множество точек
, то множество точек  , удовлетворяющих неравенству
, удовлетворяющих неравенству 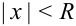 , называется интервалом сходимости I степенного ряда. Значит, если
, называется интервалом сходимости I степенного ряда. Значит, если 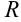 — радиус сходимости степенного ряда
— радиус сходимости степенного ряда  , то его интервал сходимости находится следующим образом:
, то его интервал сходимости находится следующим образом: 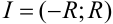 .
.
Так, интервалом сходимости степенного ряда 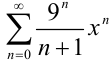 , рассмотренного в примере 35.2., будет
, рассмотренного в примере 35.2., будет 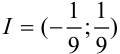 , т.к.
, т.к. 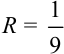 . Интервалом сходимости степенного ряда
. Интервалом сходимости степенного ряда 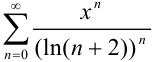 , рассмотренного в примере 35.3., будет
, рассмотренного в примере 35.3., будет 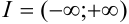 , т.к.
, т.к. 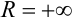 (данный ряд сходится во всех точках числовой оси).
(данный ряд сходится во всех точках числовой оси).
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Свойства абсолютно сходящихся рядов. |
| Понятие функционального ряда. |
| Область сходимости степенного ряда. |
| Свойства степенных рядов. |

