Пусть задана бесконечная последовательность функций 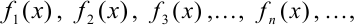 определённых на одном и том же множестве
определённых на одном и том же множестве 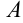 . Ряд вида
. Ряд вида 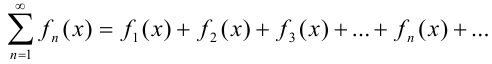 , членами которого являются функции от
, членами которого являются функции от  , называется функциональным. По определению, ряды
, называется функциональным. По определению, ряды 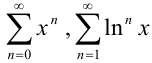 — функциональные. Придавая
— функциональные. Придавая  определенное значение
определенное значение 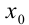 из множества
из множества 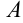 , получим числовой ряд
, получим числовой ряд 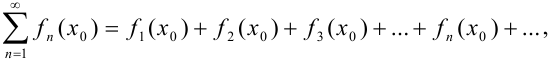 который может оказаться как сходящимся, так и расходящимся. Если полученный числовой ряд сходится, то точка
который может оказаться как сходящимся, так и расходящимся. Если полученный числовой ряд сходится, то точка 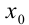 называется точкой сходимости функционального ряда
называется точкой сходимости функционального ряда 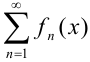 ; если же числовой ряд расходится — точкой расходимости функционального ряда.
; если же числовой ряд расходится — точкой расходимости функционального ряда.
Пример №35.1.
Докажите, что точка 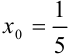 является точкой сходимости, а
является точкой сходимости, а 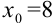 — точкой расходимости функционального ряда
— точкой расходимости функционального ряда 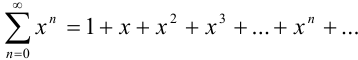
Доказательство. Подставим в функциональный ряд 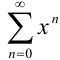 , вместо
, вместо 
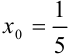 . Получим числовой ряд
. Получим числовой ряд 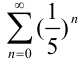 , который является сходящимся рядом геометрической прогрессии (лекция 33). Следовательно, по определению,
, который является сходящимся рядом геометрической прогрессии (лекция 33). Следовательно, по определению, 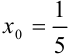 — точка сходимости функционального ряда
— точка сходимости функционального ряда 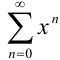 .
.
Подставим в функциональный ряд 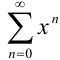 , вместо
, вместо 
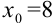 . Получим числовой ряд
. Получим числовой ряд 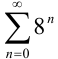 , который является расходящимся рядом геометрической прогрессии (лекция 33). Следовательно, по определению,
, который является расходящимся рядом геометрической прогрессии (лекция 33). Следовательно, по определению, 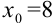 — точка расходимости функционального ряда
— точка расходимости функционального ряда 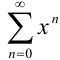 , что и требовалось доказать.
, что и требовалось доказать.
Множество всех точек сходимости функционального ряда 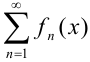 называется его областью сходимости. В области сходимости функционального ряда
называется его областью сходимости. В области сходимости функционального ряда 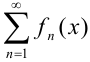 его сумма является некоторой функцией от
его сумма является некоторой функцией от  :
: 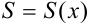 . Определяется она в области сходимости равенством:
. Определяется она в области сходимости равенством: 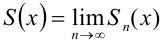 , где
, где 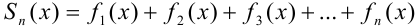 — частичная сумма ряда.
— частичная сумма ряда.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Абсолютная и условная сходимость знакочередующегося ряда. |
| Свойства абсолютно сходящихся рядов. |
| Понятие степенного ряда. Радиус и интервал сходимости. |
| Область сходимости степенного ряда. |

