В некоторых ситуациях, когда ни один из признаков сравнения, Даламбера, Коши не дает ответ о сходимости положительного ряда, исследовать ряд на сходимость позволяет интегральный признак Коши. Сформулируем его без доказательства.
Интегральный признак Коши: Если члены положительного ряда 
могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке 
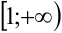функции 
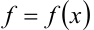так, что 
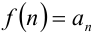, то данный ряд и несобственный интеграл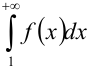 
одновременно сходятся или расходятся.
Заметим, что вместо интеграла 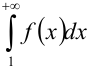можно брать интеграл 
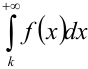, где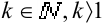 
. Это связано с тем, что отбрасывание 
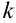первых членов ряда не влияет, в силу свойства числовых рядов (свойство 1 лекции 32), на его сходимость (расходимость).
Пример №33.7.
Исследуйте ряд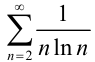 
на сходимость, применяя интегральный признак Коши.
Решение:
Рассмотрим функцию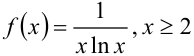 
. Эта функция непрерывна, монотонно убывает на 
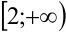, и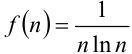 
, следовательно, можно применить интегральный признак Коши. Выясним, будет ли несобственный интеграл 
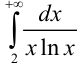сходиться или расходиться.
Имеем: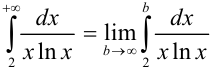 
.
Отдельно найдем неопределенный интеграл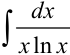 
методом замены переменной:
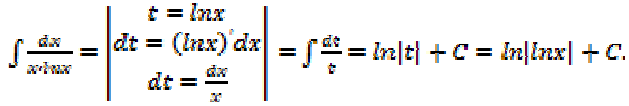
Найдем предел: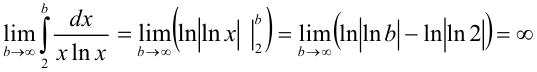 
Таким образом, получили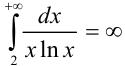 
. Следовательно, несобственный интеграл 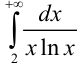расходится. Значит, в силу интегрального признака Коши, ряд 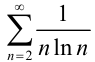также будет расходиться.
Ответ: 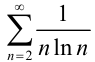расходится.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Признак Даламбсра. |
| Признак Коши (радикальный). |
| Понятие знакочередующегося ряда. Признак Лейбница. |
| Абсолютная и условная сходимость знакочередующегося ряда. |
