Оглавление:
При изучении многих практических вопросов естествознания и техники применяется метод поэтапного исследования данного объекта. На первом этапе учитываются самые главные характеристики изучаемого процесса, явления. Так выполняется этап первого приближения. Затем переходят к следующему этапу, учитывая новые или более точно старые характеристики предмета.
Одним из математических понятий, при помощи которых моделируются такие ситуации, является понятие «суммы» бесконечного числа слагаемых. Именно за этим понятием утвердилось название ряда.
Пусть задана бесконечная числовая последовательность 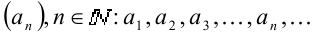 . Выражение вида
. Выражение вида 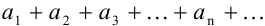 называется числовым рядом. Числа
называется числовым рядом. Числа  называются членами ряда (соответственно первым, вторым и т.д. ,
называются членами ряда (соответственно первым, вторым и т.д. , 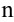 -м или общим).
-м или общим).
Для сокращенного обозначения ряда используется знак суммирования 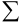 , а именно:
, а именно:
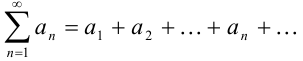
Ряд считается заданным, если известен общий член ряда 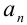 , выраженный как функция его номера
, выраженный как функция его номера 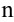 :
: 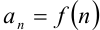 . Так, ряд
. Так, ряд 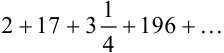 нельзя считать заданным, поскольку общий член ряда нельзя выразить формулой. Ряд 2 + 5 + 8 + 11 + 14 + … можно считать заданным, т.к. его общий член выражается формулой:
нельзя считать заданным, поскольку общий член ряда нельзя выразить формулой. Ряд 2 + 5 + 8 + 11 + 14 + … можно считать заданным, т.к. его общий член выражается формулой: 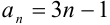 . Таким образом,
. Таким образом,
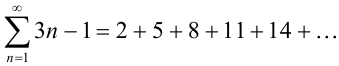
Для заданного ряда легко можно найти любой его член. Это осуществляется путем подстановки в формулу общего члена ряда номера искомого члена.
Пример №32.1.
Выпишите четыре первых члена ряда 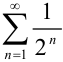 .
.
Решение:
Общий член заданного ряда выражается формулой 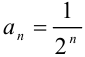 . Тогда первый член ряда
. Тогда первый член ряда 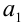 найдем путем подстановки в эту формулу значения
найдем путем подстановки в эту формулу значения 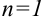 , т.е.
, т.е. 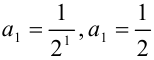 . По аналогии найдем второй, третий и четвертый члены ряда:
. По аналогии найдем второй, третий и четвертый члены ряда:
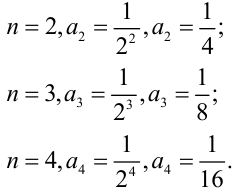
Таким образом, можно записать: 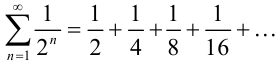
Ответ: 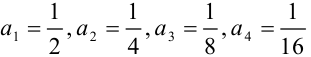 или
или 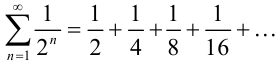
Рассмотренный в примере 32.1. ряд является рядом геометрической прогрессии.
Специфическое название — гармонический имеет ряд, составленный из чисел, обратных натуральным, т.е. 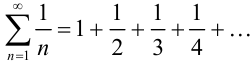
При анализе рядов, полученных в результате моделирования какой-нибудь конкретной задачи, важнейшим является вопрос стабилизируемости моделируемого процесса. Ответ на него напрямую зависит от того, имеет ли ряд сумму. Если ряд имеет сумму, значит, процесс стабилизируется, в противном случае — нет.
Рассмотрим ряд 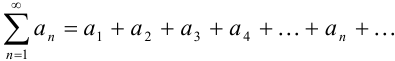
Будем последовательно складывать его члены:
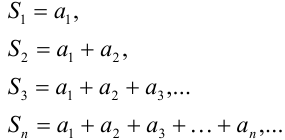
Полученные суммы называются частичными суммами ряда. Таким образом, будем иметь бесконечную числовую последовательность частичных сумм ряда 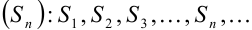 . Рассмотрим ее предел
. Рассмотрим ее предел 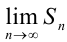 . Он может существовать или не существовать. В зависимости от этого ряд может быть сходящимся или расходящимся.
. Он может существовать или не существовать. В зависимости от этого ряд может быть сходящимся или расходящимся.
Ряд  называется сходящимся, если существует конечный предел последовательности частичных сумм ряда, т.е.
называется сходящимся, если существует конечный предел последовательности частичных сумм ряда, т.е. 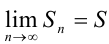 . Данный предел называют суммой ряда. Таким образом, сходящийся ряд имеет сумму (ему можно приписать конкретное число). Часто этот факт записывают в следующей форме:
. Данный предел называют суммой ряда. Таким образом, сходящийся ряд имеет сумму (ему можно приписать конкретное число). Часто этот факт записывают в следующей форме: 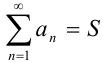 .
.
Ряд  называется расходящимся, если предел последовательности частичных сумм равен бесконечности или вовсе нс существует. Такой ряд суммы не имеет. Расходящемуся ряду нельзя приписать конкретное число. Этот факт часто выражают в следующей форме:
называется расходящимся, если предел последовательности частичных сумм равен бесконечности или вовсе нс существует. Такой ряд суммы не имеет. Расходящемуся ряду нельзя приписать конкретное число. Этот факт часто выражают в следующей форме: 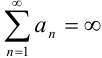 .
.
Поскольку важнейшей задачей теории рядов является исследование их сходимости, рассмотрим ее решение по определению (с помощью анализа последовательности частичных сумм) на конкретных примерах.
Пример №32.2.
Исследуйте ряд 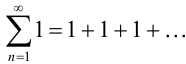 на сходимость по определению (с помощью анализа последовательности его частичных сумм).
на сходимость по определению (с помощью анализа последовательности его частичных сумм).
Решение:
Найдем частичные суммы ряда 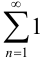 :
:
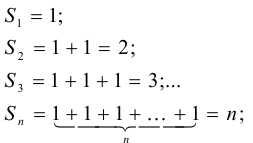
Рассмотрим последовательность 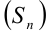 частичных сумм ряда:
частичных сумм ряда: 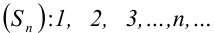 Найдем ее предел:
Найдем ее предел: 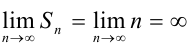 . Следовательно, по определению, ряд
. Следовательно, по определению, ряд 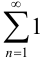 расходится.
расходится.
Ответ: 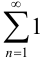 расходится.
расходится.
Пример №32.3.
Исследуйте ряд 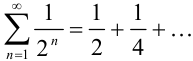 на сходимость по определению (с помощью анализа последовательности его частичных сумм).
на сходимость по определению (с помощью анализа последовательности его частичных сумм).
Решение:
Данный ряд, являясь рядом геометрической прогрессии, представляет собой бесконечно убывающую геометрическую прогрессию 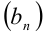 с
с 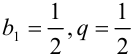 . Как известно, сумма первых
. Как известно, сумма первых 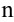 членов такой прогрессии находится по формуле:
членов такой прогрессии находится по формуле: 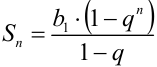 . Тогда в нашем случае для частичных сумм данного ряда имеем:
. Тогда в нашем случае для частичных сумм данного ряда имеем: 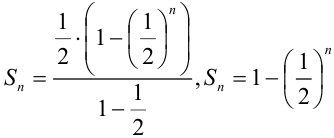 . Найдем предел последовательности частичных сумм ряда:
. Найдем предел последовательности частичных сумм ряда: 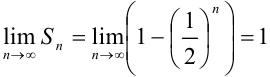 . Следовательно, по определению, ряд
. Следовательно, по определению, ряд 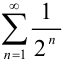 сходится, и его сумма равна 1, т.е.
сходится, и его сумма равна 1, т.е. 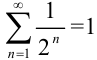 .
.
Ответ: 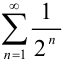 сходится
сходится 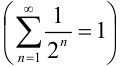 .
.
В приведенных примерах последовательности 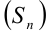 частичных сумм или находились довольно-таки просто или выражались заранее. В большинстве случаев непосредственный анализ последовательности
частичных сумм или находились довольно-таки просто или выражались заранее. В большинстве случаев непосредственный анализ последовательности 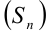 частичных сумм ряда не представляется возможным.
частичных сумм ряда не представляется возможным.
Поэтому основной задачей теории рядов является установление их сходимости или расходимости без использования последовательности 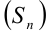 . Первый механизм в ее решении — применение свойств числовых рядов.
. Первый механизм в ее решении — применение свойств числовых рядов.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Геометрический смысл двойного интеграла от единичной функции. |
| Вычисление площадей плоских фигур с помощью двойного интеграла. |
| Свойства числовых рядов. |
| Необходимый признак сходимости ряда. |

