Оглавление:
Рассмотрим примеры вычисления площадей плоских фигур с помощью двойного интеграла.
Пример №31.1.
Найдите площадь плоской фигуры, ограниченной линиями 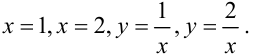
Решение:
Поскольку геометрически двойной интеграл от единичной функции по области  равен площади плоской фигуры, представляющей собой область интегрирования
равен площади плоской фигуры, представляющей собой область интегрирования  , будем использовать формулу:
, будем использовать формулу: 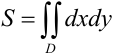 .
.
В нашем случае областью интегрирования  является фигура, ограниченная линиями
является фигура, ограниченная линиями 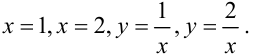 Вычислим
Вычислим 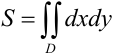 .
.
Для этого построим область интегрирования  в прямоугольной декартовой системе координат на плоскости.
в прямоугольной декартовой системе координат на плоскости.
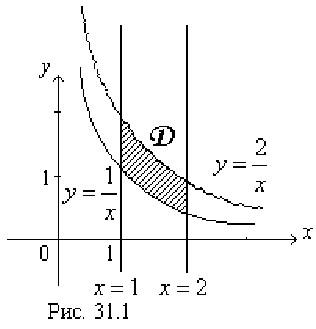
Линии, задаваемые уравнениями 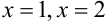 , — прямые, параллельные оси
, — прямые, параллельные оси 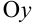 и проходящие соответственно через точки (1;0), (2;0). Линия, задаваемая уравнением
и проходящие соответственно через точки (1;0), (2;0). Линия, задаваемая уравнением 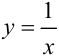 — гипербола, «ветви» которой расположены в I и III координатных четвертях. Гиперболу
— гипербола, «ветви» которой расположены в I и III координатных четвертях. Гиперболу 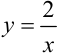 можно получить из гиперболы
можно получить из гиперболы 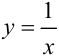 с помощью растяжения последней вдоль оси ординат в два раза.
с помощью растяжения последней вдоль оси ординат в два раза.
Описание линий, задающих область интегрирования  , позволяет при ее построении ограничиться I координатной четвертью.
, позволяет при ее построении ограничиться I координатной четвертью.
Изображенная на рис. 31.1 область интегрирования  является криволинейной областью I типа. Поэтому для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:
является криволинейной областью I типа. Поэтому для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:
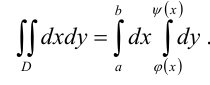
В нашем случае 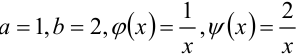 . Следовательно,
. Следовательно, 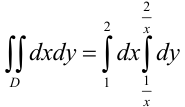 .
.
Вычислим полученный повторный интеграл:
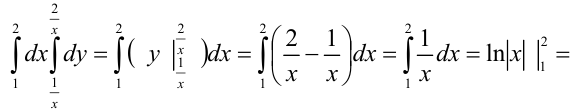
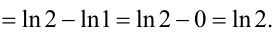
В итоге, 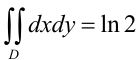 . Следовательно,
. Следовательно, 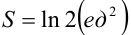 .
.
Ответ: 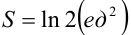 .
.
Пример №31.2.
Найдите площадь плоской фигуры, ограниченной линиями 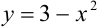 и
и 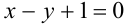 .
.
Решение:
Плоскую фигуру, ограниченную линиями 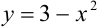 и
и 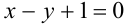 , обозначим
, обозначим  . В силу геометрического смысла двойного интеграла от единичной функции, для нахождения площади
. В силу геометрического смысла двойного интеграла от единичной функции, для нахождения площади 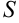 плоской фигуры
плоской фигуры  будем использовать формулу:
будем использовать формулу: 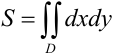 .
.
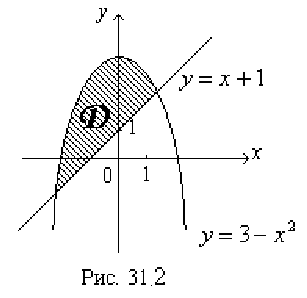
Вычислим 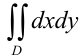 . Для этого построим фигуру
. Для этого построим фигуру  (рис. 31.2), представляющую собой область интегрирования, в прямоугольной декартовой системе координат на плоскости.
(рис. 31.2), представляющую собой область интегрирования, в прямоугольной декартовой системе координат на плоскости.
Линия, задаваемая уравнением 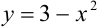 — парабола, «ветви» которой направлены вниз. Построим ее с помощью параллельного переноса вдоль оси ординат графика функции
— парабола, «ветви» которой направлены вниз. Построим ее с помощью параллельного переноса вдоль оси ординат графика функции 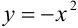 на 3 единицы вверх. Линия, задаваемая уравнением
на 3 единицы вверх. Линия, задаваемая уравнением 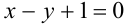 — прямая. Составим уравнение прямой с угловым коэффициентом:
— прямая. Составим уравнение прямой с угловым коэффициентом: 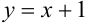 .
.
Построим эту прямую по двум точкам:
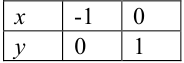
Изображенная на рис. 31.2. область интегрирования  является криволинейной областью I типа. Поэтому для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:
является криволинейной областью I типа. Поэтому для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу: 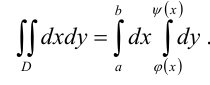
В нашем случае 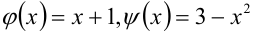 . Найдем
. Найдем 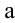 и
и 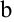 как абсциссы точек пересечения линий
как абсциссы точек пересечения линий 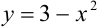 и
и 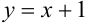 . Для этого решим уравнение
. Для этого решим уравнение 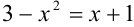 . Корни приведенного квадратного уравнения
. Корни приведенного квадратного уравнения 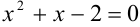 найдем по теореме, обратной теореме Виета:
найдем по теореме, обратной теореме Виета: 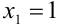 или
или 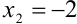 . Следовательно,
. Следовательно, 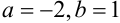 . Таким образом,
. Таким образом, 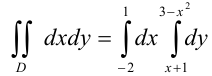 . Вычислим полученный повторный интеграл:
. Вычислим полученный повторный интеграл:
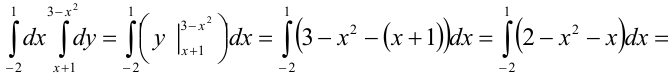
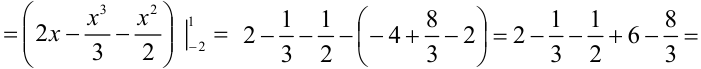
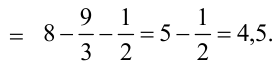
В итоге, 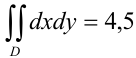 . Следовательно,
. Следовательно, 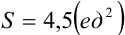 .
.
Ответ: 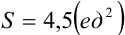 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Вычисление объемов геометрических тел с помощью двойного интеграла. |
| Геометрический смысл двойного интеграла от единичной функции. |
| Определение числового ряда. |
| Свойства числовых рядов. |

