Вычисление двойного интеграла сведением его к повторному

Двойной интеграл вычисляется путем сведения его к повторному с применением соответствующей формулы. Вид формулы, по которой осуществляется сведение, зависит от типа области интегрирования. Различают три типа области интегрирования: прямоугольную, криволинейную I типа и криволинейную II типа. Поэтому при вычислении двойного интеграла возникают три ситуации. Рассмотрим их, опуская собственно вывод формул
сведения двойного интеграла к повторному.

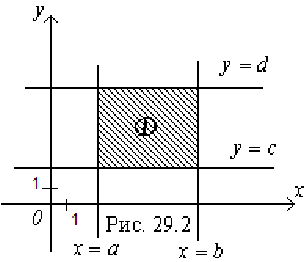
1. Область интегрирования на плоскости 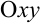является прямоугольной. т.е. ограничена прямыми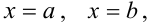 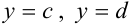, причем 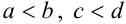(рис. 29.2.). В этом случае формула сведения двойного интеграла к повторному имеет вид:

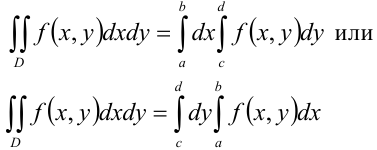
2. Область интегрирования на плоскости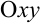
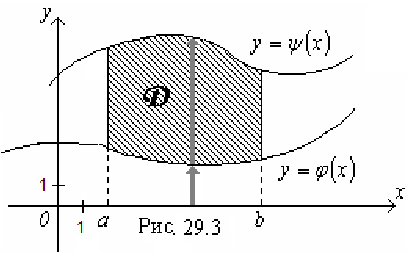
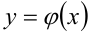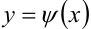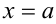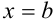является криволинейной областью I типа, т.е. ограничена снизу и сверху непрерывными кривыми и , а слева и справа -отрезками прямых и так, что любая прямая, параллельная оси 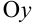и проходящая внутри отрезка 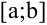пересекает границу области (кривые 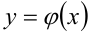и 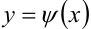) в двух точках (рис 29.3.).
В этом случае формула сведения двойного интеграла к повторному имеет вид:

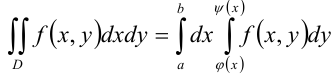
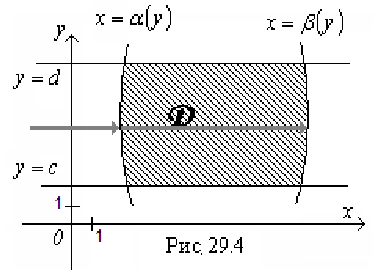
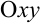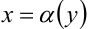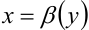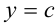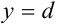3. Область интегрирования на плоскости является криволинейной областью II типа, т.е. ограничена слева и справа непрерывными кривыми и , а снизу и сверху — отрезками прямых и так, что любая прямая, параллельная оси 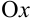и проходящая внутри отрезка 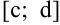, пересекает границу области (кривые 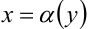и 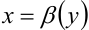) в двух точках (рис. 29.4.). В этом случае формула сведения двойного интеграла к повторному имеет вид:

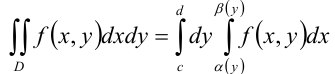
Таким образом, при вычислении двойных интегралов удобно использовать следующий алгоритм:

1. Построить область интегрирования в прямоугольной декартовой системе координат на плоскости (исключением может быть случай прямоугольной области).
2. Определить тип области и в соответствии с ним составить формулу сведения двойного интеграла к повторному.
3. Вычислить полученный повторный интеграл.

Рассмотрим примеры вычисления двойных интегралов.

Пример №29.2.

Вычислите двойной интеграл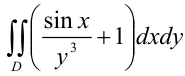
по прямоугольной области , ограниченной прямыми .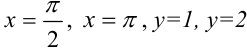

Решение:

1.Область интегрирования является прямоугольной. Для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:

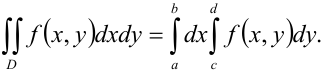
В нашем случае 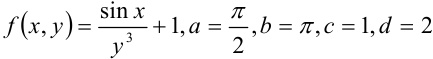. Следовательно,

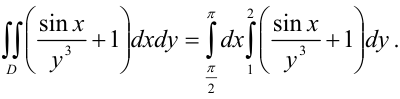
2. Вычислим полученный повторный интеграл:

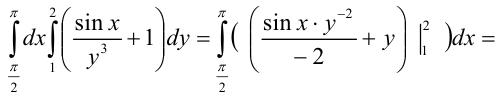
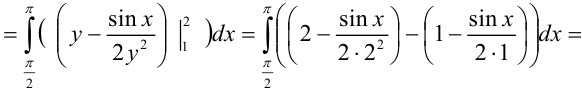
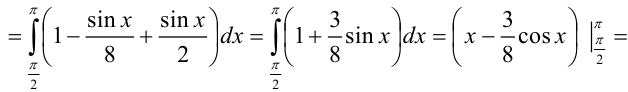
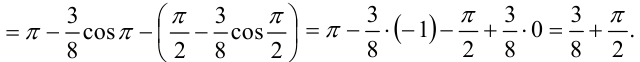
Таким образом, окончательно имеем:

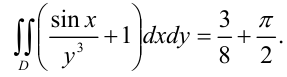
Этот двойной интеграл по прямоугольной области можно вычислить также использованием формулы

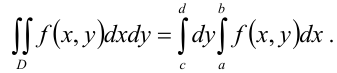
Тогда .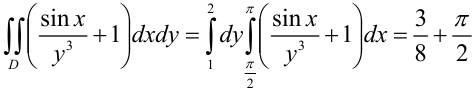

Ответ: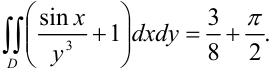

Пример №29.3.

Вычислите двойной интеграл 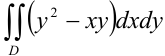по области , ограниченной линиям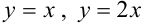и и .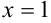

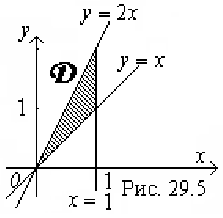
Решение:

1) Построим область интегрирования в прямоугольной декартовой системе координат на плоскости (рис. 29.5.). Линия, задаваемая уравнением 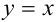, — прямая, являющаяся биссектрисой I и III координатных углов.

Линия, задаваемая уравнением 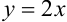, — прямая. Построим ее по двум точкам:

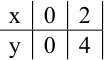
Линия, задаваемая уравнением 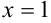, — прямая, параллельная оси 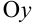и проходящая через точку (1; 0).

В итоге, область интегрирования обозначена на рис. 29.5. штриховкой.

2) Область интегрирования является криволинейной областью I типа. Для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:

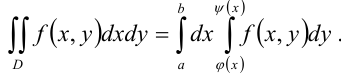
В нашем случае 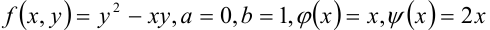. Следовательно,

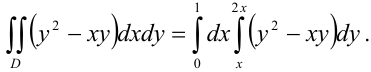
3) Вычислим полученный повторный интеграл:

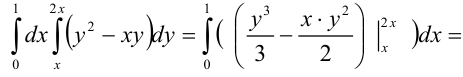
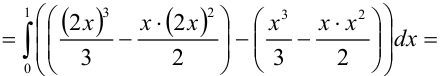
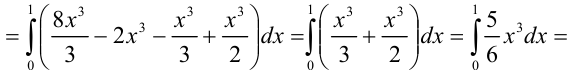
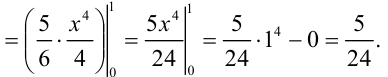
Таким образом, окончательно имеем:

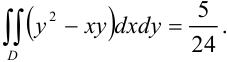
Ответ: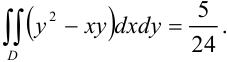

Пример №29.4.

Вычислите двойной интеграл 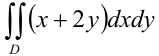по области , ограниченной линиями .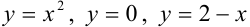

Решение:

1) Построим область интегрирования в прямоугольной декартовой системе координат на плоскости. Линия, задаваемая уравнением 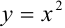, — парабола с вершиной в начале координат, «ветви» которой направлены вверх. Линия, задаваемая уравнением 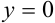, — ось абсцисс. Линия, задаваемая уравнением 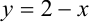, — прямая. Построим ее по двум точкам:

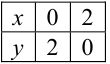
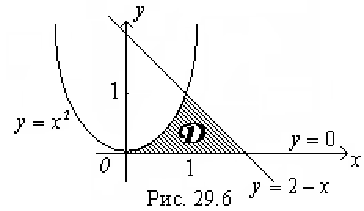
В итоге, область интегрирования обозначена на рис. 29.6. штриховкой.

2) Область интегрирования является криволинейной областью II типа. Для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:

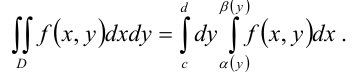
В нашем случае очевидно 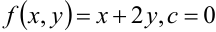. Найдем 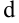как ординату точки пересечения графиков функци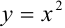й и 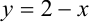в первой координатной четверти. Предварительно вычислим абсциссу точки пересечения графиков, решив уравнение 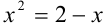. По теореме, обратной теореме Виста для приведенного квадратного уравнения 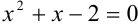, получим корни 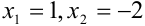. В первой координатной четверти находится точка с абсциссой 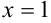. Ее ординату найдем, подставляя 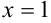в уравнение 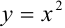. Отсюда .

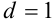Выражая 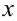из уравнени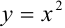й и 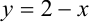, получим соответственно 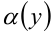и 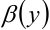. Так, 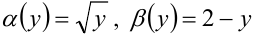. Следовательно, .

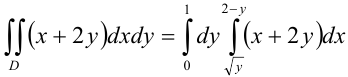3) Вычислим полученный повторный интеграл:

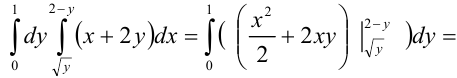
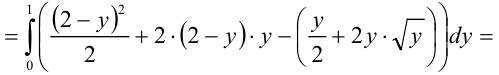
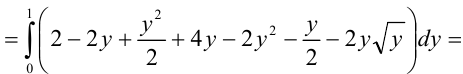
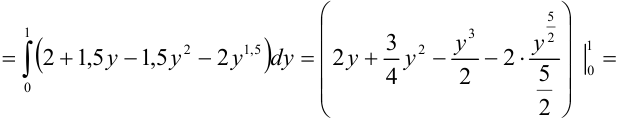
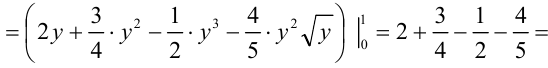
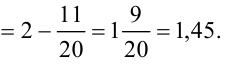
Таким образом, окончательно имеем:

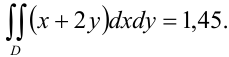
Ответ: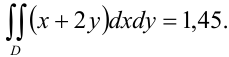

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Свойства двойных интегралов.

Понятие повторного интеграла.

Геометрический смысл двойного интеграла.

Вычисление объемов геометрических тел с помощью двойного интеграла.