Вычислять двойные интегралы как пределы интегральных сумм весьма затруднительно, поэтому возникает естественная задача о разработке техники двойного интегрирования, минуя непосредственное суммирование и предельный переход.
Важнейшим результатом в этом направлении является формула сведения двойного интеграла к повторному. Определим понятие повторного интеграла.
Пусть на отрезке 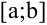 заданы непрерывные функции
заданы непрерывные функции 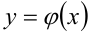 и
и 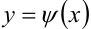 такие, что
такие, что 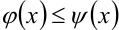 ,
, 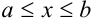 , и пусть на области
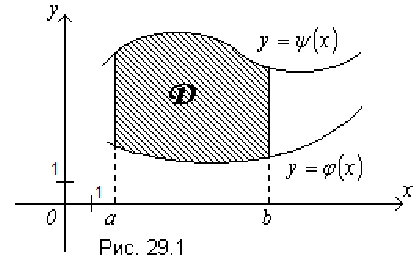
, и пусть на области 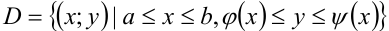 (рис.29.1.) определена функция
(рис.29.1.) определена функция  .
.
Если для любого фиксированного 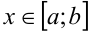 функция
функция  , как функция переменной
, как функция переменной  , интегрируема на отрезке
, интегрируема на отрезке 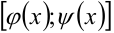 , т.е. при любом
, т.е. при любом 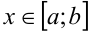 существует интеграл
существует интеграл 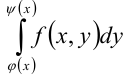 , и функция
, и функция 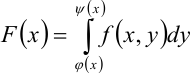 интегрируема на отрезке
интегрируема на отрезке 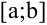 , то интеграл
, то интеграл 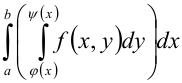 называется повторным интегралом и
называется повторным интегралом и
обозначается через 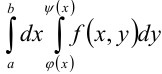 .
.
При этом 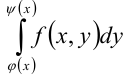 называется внутренним интегралом;
называется внутренним интегралом;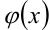 и
и 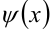 — внутренними,
— внутренними, 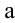 и
и 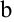 — внешними пределами интегрирования. Если внутренние пределы интегрирования в повторном интеграле могут быть как постоянными, так и переменными, то внешние пределы постоянны всегда.
— внешними пределами интегрирования. Если внутренние пределы интегрирования в повторном интеграле могут быть как постоянными, так и переменными, то внешние пределы постоянны всегда.
Для вычисления повторного интеграла 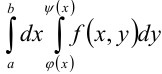 надо последовательно взять два обычных определенных интеграла. Сначала берется внутренний интеграл
надо последовательно взять два обычных определенных интеграла. Сначала берется внутренний интеграл 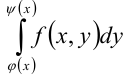 , в котором переменная
, в котором переменная 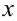 считается постоянной. Затем берется внешний интеграл, т.е. полученное выражение, зависящее от
считается постоянной. Затем берется внешний интеграл, т.е. полученное выражение, зависящее от 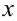 , интегрируется по
, интегрируется по 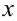 от
от 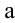 до
до 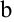 .
.
Рассмотрим пример вычисления повторного интеграла.
Пример №29.1.
Вычислите повторный интеграл 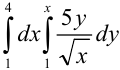 .
.
Решение:
Сначала найдем внутренний интеграл, считая 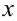 постоянным:
постоянным:
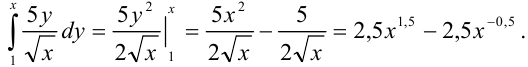
Затем найдем внешний интеграл, т.е. полученную функцию проинтегрируем по 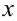 . Тогда
. Тогда
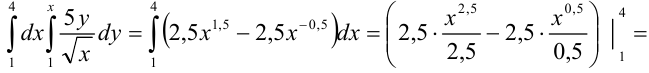
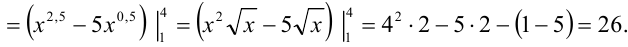
Для сокращения записи все вычисления можно записать следующим образом:
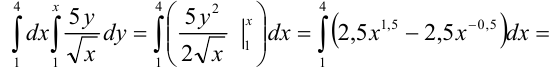
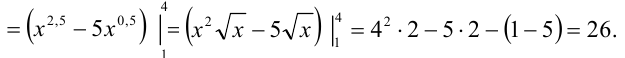
Ответ: 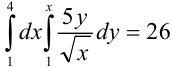 .
.
Следует заметить, что для функции  , определенной на области
, определенной на области 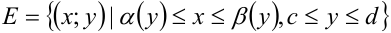 понятие повторного интеграла вводится аналогично рассмотренному ранее. При этом повторный интеграл обозначается через
понятие повторного интеграла вводится аналогично рассмотренному ранее. При этом повторный интеграл обозначается через 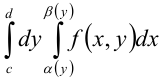 .
.
Здесь при вычислении внутреннего интеграла постоянной считается переменная 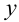 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие двойного интеграла. |
| Свойства двойных интегралов. |
| Вычисление двойного интеграла сведением его к повторному. |
| Геометрический смысл двойного интеграла. |

