Поскольку процесс построения интеграла в области  практически дословно повторяет процедуру определения интеграла функции одной переменной на отрезке (лекция 21 части 1), свойства этих интегралов, как и доказательства свойств, аналогичны. Поэтому перечислим основные свойства двойных интегралов, считая подынтегральные функции интегрируемыми.
практически дословно повторяет процедуру определения интеграла функции одной переменной на отрезке (лекция 21 части 1), свойства этих интегралов, как и доказательства свойств, аналогичны. Поэтому перечислим основные свойства двойных интегралов, считая подынтегральные функции интегрируемыми.
1. Постоянный множитель можно выносить за знак двойного интеграла:
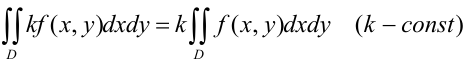
2. Двойной интеграл от алгебраической суммы двух функций равен алгебраической сумме двойных интегралов от этих функций:
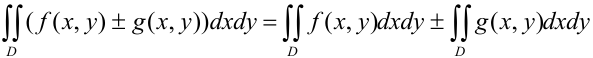
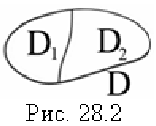
3. Если область  разбить линией на две области
разбить линией на две области 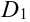 и
и 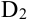 такие, что
такие, что 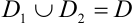 , а пересечение
, а пересечение 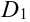 и
и 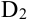 состоит лишь из линии, их разделяющей (рис. 28.2), то
состоит лишь из линии, их разделяющей (рис. 28.2), то
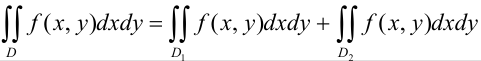
4. Если в области  имеет место неравенство
имеет место неравенство 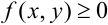 , то и
, то и 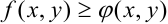 . Если в области
. Если в области  функции
функции  и
и 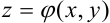 удовлетворяют неравенству
удовлетворяют неравенству 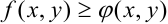 , то
, то
и
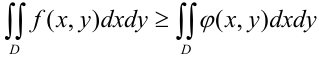
5. В силу 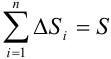 ,
, 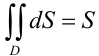 .
.
6. Если функция  непрерывна в замкнутой области
непрерывна в замкнутой области  , площадь которой
, площадь которой 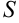 , то
, то 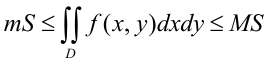 , где
, где 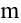 и
и 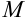 — соответственно наименьшее и наибольшее значения подынтегральной функции в области
— соответственно наименьшее и наибольшее значения подынтегральной функции в области  .
.
7. Если функция  непрерывна в замкнутой области
непрерывна в замкнутой области  , площадь которой
, площадь которой 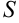 , то в этой области существует такая точка
, то в этой области существует такая точка 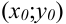 , что
, что 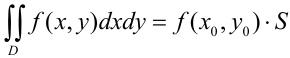 . Величину
. Величину
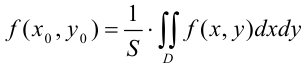
называют средним значением функции  в области
в области  .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие дифференциала высших порядков функции нескольких переменных. |
| Понятие двойного интеграла. |
| Понятие повторного интеграла. |
| Вычисление двойного интеграла сведением его к повторному. |
