Двойной интеграл является своеобразным обобщением определенного интеграла на случай функции двух переменных.
Пусть в замкнутой области 
плоскости 
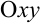задана непрерывная функция 
. График этой функции представляет собой некоторую поверхность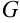 
, ограничивающую цилиндрическое тело с основание .
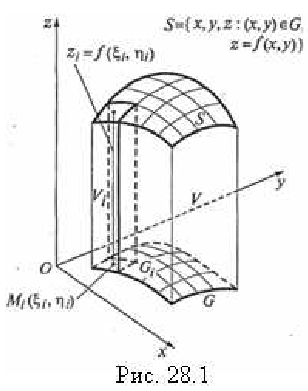
Осуществим следующие действия (рис. 28.1):
1. Разобьем область линиями на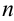 
элементарных областей 
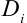с площадями 
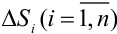. Диаметр (наибольшее расстояние между точками элементарной области) обозначим через 
.
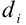2. В каждой из элементарных областей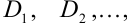 
выберем соответственно произвольную точку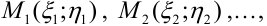 
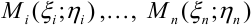
3. Найдем значения функции в точках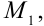 
: 
.
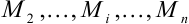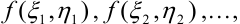
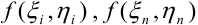4. Для каждой элементарной области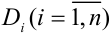 
умножим найденное значение функции 
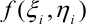на площадь соответствующей области 
.
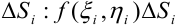5. Составим сумму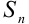 
всех таких произведений:
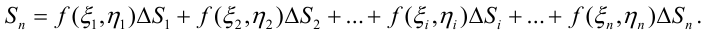
Такую сумму называют интегральной суммой функции в области .
Если в замкнутой области функция принимает значения, то каждое слагаемое интегральной суммы равно объему столбика с основанием 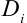и высотой 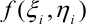, ограниченного сверху куском поверхности неотрицательные цилиндрического
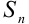. Тогда вся сумма равна объему «ступенчатого тела», получающегося объединением рассматриваемых цилиндрических столбиков.
Мы разбивали области на произвольное число элементарных областей, точку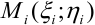 
внутри каждой элементарной области также выбирали произвольно. Очевидно, что при различных разбиениях области и различном выборе точек 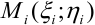можно составить бесконечное число интегральных сумм.
Найдем предел интегральной суммы 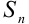при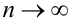 
, но при условии, что наибольший из диаметров элементарных областей будет стремиться к нулю, то есть 
.
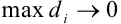Если пр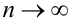и и 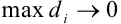интегральная сумма 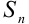имеет предел, который не зависит ни от способа разбиения области на элементарные области, ни от выбора точек 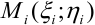в них, то этот предел называется двойным интегралом от функции по области и обозначается
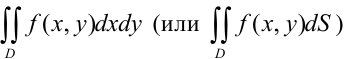
Таким образом, двойной интеграл определяется равенством:
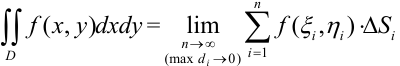
В этом случае называется областью интегрирования, 
и 
— переменными интегрирования,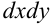 
(или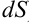 
) — элементом площади.
Функция , для которой в области существует двойной интеграл, называется интегрируемой в этой области.
Сформулируем теорему существования двойного интеграла (или достаточное условие интегрируемости функции).
Теорема. Если функция непрерывна в замкнутой области , то она интегрируема в этой области.
В дальнейшем будем предполагать, что условия этой теоремы для рассматриваемых нами функций выполнены.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
