С помощью частных производных высших порядков вводятся дифференциалы высших порядков функции двух действительных переменных. Как и частные производные, они определяются последовательно.
Рассмотрим функцию  двух действительных переменных, обладающую непрерывными частными производными второго порядка. Ее полный дифференциал
двух действительных переменных, обладающую непрерывными частными производными второго порядка. Ее полный дифференциал 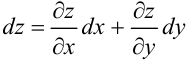 называют полным дифференциалом первого порядка (или, кратко, первым дифференциалом).
называют полным дифференциалом первого порядка (или, кратко, первым дифференциалом).
Поскольку 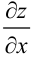 и
и 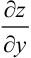 по предположению имеют непрерывные частные производные первого порядка, то от функции
по предположению имеют непрерывные частные производные первого порядка, то от функции 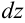 , в свою очередь, можно взять полный дифференциал
, в свою очередь, можно взять полный дифференциал 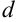 (
(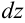 ). Таким образом, получим полный дифференциал второго порядка (или, кратко, второй дифференциал). который обозначается
). Таким образом, получим полный дифференциал второго порядка (или, кратко, второй дифференциал). который обозначается 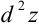 .
.
Дифференциалом второго порядка функции  называется дифференциал от первого дифференциала:
называется дифференциал от первого дифференциала:
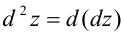
Аналогично, потребовав существование непрерывных частных производных третьего, четвертого, …, 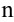 -го порядков, можно определить дифференциалы соответственно третьего,
-го порядков, можно определить дифференциалы соответственно третьего,
четвертого, …, 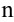 -го порядков.
-го порядков.
Так, дифференциалом 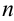 -го порядка функции
-го порядка функции  называется дифференциал от дифференциала
называется дифференциал от дифференциала 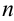 -1 порядка:
-1 порядка:
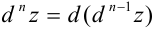
Найдем формулу для вычисления дифференциала второго порядка:
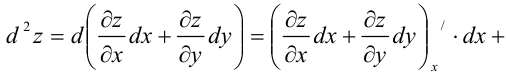
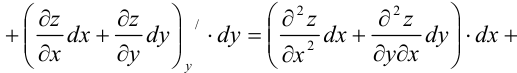
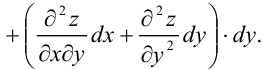
Отсюда: 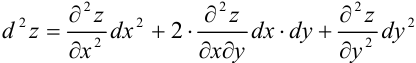 . Символически это записывается так:
. Символически это записывается так:
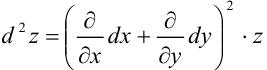
Этот символ расшифровывается следующим образом. Сначала раскрываются скобки, как будто слагаемые в них числа, а число 2 — показатель степени. Затем числители полученных дробей умножаются на 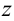 .
.
Формула для 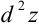 обобщается на случай
обобщается на случай 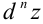 :
:
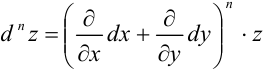
Этот символ расшифровывается так же, как и для 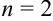 .
.
Отметим, что полученные формулы справедливы лишь тогда, когда переменные  и
и  функции
функции  являются независимыми.
являются независимыми.
Рассмотрим пример нахождения дифференциала второго прядка функции.
Пример №27.4.
Найдите дифференциал второго порядка функции 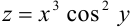 .
.
Решение:
Найдем 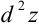 по формуле:
по формуле: 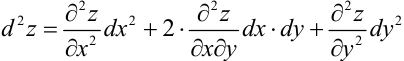 .
.
Сначала найдем частные производные первого порядка функции:
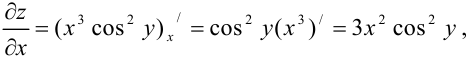
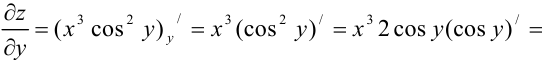
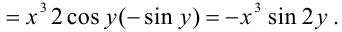
Затем найдем частные производные второго порядка функции:
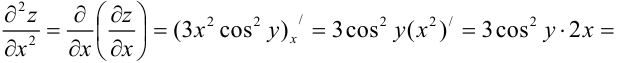
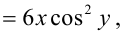
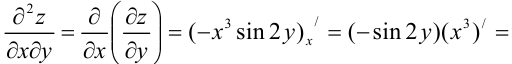
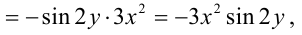
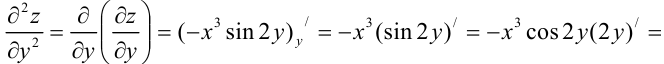
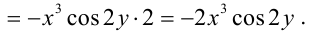
Окончательно получим:
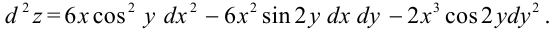
Ответ: 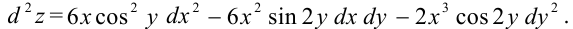
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:

