Геометрический смысл определенного интеграла связан с понятием криволинейной трапеции.
Рассмотрим функцию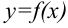 
, непрерывную на отрезке 
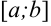и принимающую на нем неотрицательные значения (
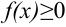). Фигуру, ограниченную сверху графиком функции 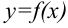, сбоку — прямыми 
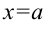и 
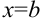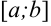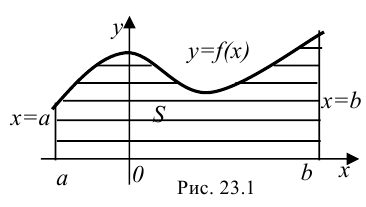
, снизу — отрезком оси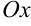 
, называют криволинейной трапецией (рис. 23.1).
Вспомним принцип введения определенного интеграла. Мы составляли интегральные суммы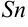 
, задающиеся формулой: 
.
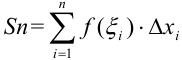Поскольку на отрезке 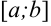функция 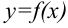принимает неотрицательные значения, то каждое слагаемое интегральной суммы равно площади прямоугольника с основанием 
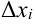и высотой 
(
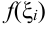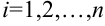). А вся сумма 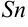равна площади «ступенчатой фигуры», получающейся объединением рассматриваемых прямоугольников (рис. 23.2).
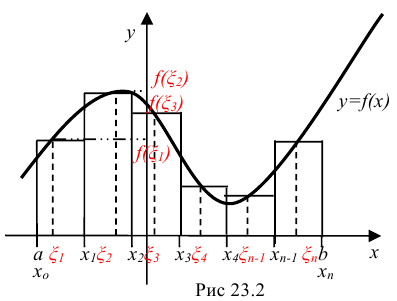
Обозначим площадь искомой криволинейной трапеции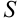 
Она приближенно будет равна площади ступенчатой фигуры : 
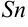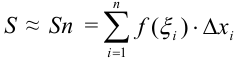. Чем меньше будет длина каждого отрезка 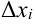, тем точнее приближение. Поэтому за точное значение площади 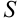криволинейной трапеции принимается предел, к которому стремится площадь ступенчатой фигуры 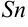, когда 
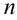неограниченно возрастает так, что 
.
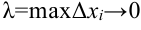Итак,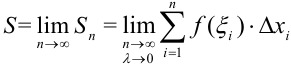 
, а это есть ни что иное, как определенный интеграл 
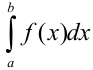. Получили, что 
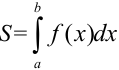. Следовательно, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции, ограниченной графиком функции 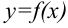, прямым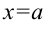и и 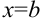, отрезком 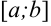оси 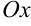. В этом и заключается геометрический смысл определенного интеграла.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
