Оглавление:
Напомним, что функция вида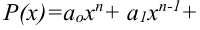 
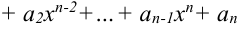, где 
, 
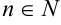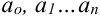— постоянные коэффициенты, называется многочленом или рациональной функцией. Число 
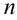называют степенью многочлена.
Дробно-рациональной функцией называется функция, равная отношению двух многочленов, т.е.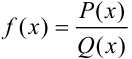 
.
Рассмотрим некоторые простейшие интегралы от дробно-рациональных функций:
1.1. Для нахождения интегралов вида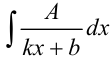 
(
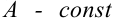) будем пользоваться интегралами от некоторых сложных функций: 
.
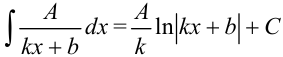Пример №20.1.
Найдите интеграл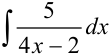 
.
Решение:
Воспользуемся приведенной выше формулой .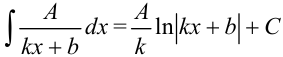
Получим, что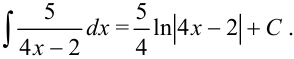 
1.2. Для нахождения интегралов вида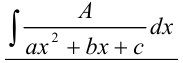 
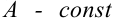() будем применять метод выделения в знаменателе полного квадрата. Исходный интеграл в результате преобразований сведется к одному из двух табличных интегралов:
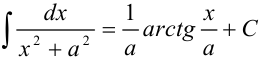или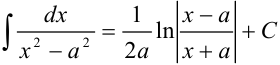 
.
Рассмотрим вычисление таких интегралов на конкретном примере.
Пример №20.2.
Найдите интеграл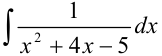 
.
Решение:
Попытаемся выделить в знаменателе полный квадрат, т.е. прийти к формуле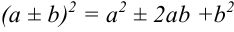 
.
Для этого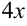 
представляем как удвоенное произведение 
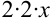. Следовательно, к выражению 
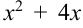чтобы получить полный квадрат следует добавить квадрат числа два, т.е. 4: 
. Но, чтобы выражение в знаменателе не изменилось, нужно из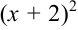 
вычесть 4. Получим следующую цепочку преобразований:
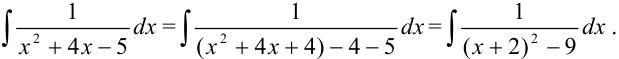
Вычислим полученный интеграл методом подстановки. Положим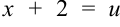 
, тогда 
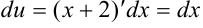. Подставим 
и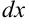 
в полученный интеграл: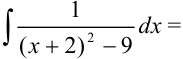 
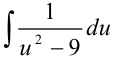. Воспользуемся табличным интегралом: 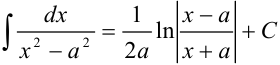, где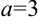 
. Получим, что 
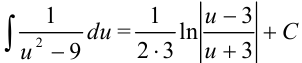. Подставим вместо выражение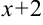 
:
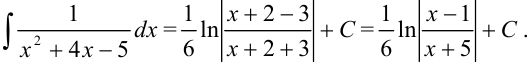
Ответ: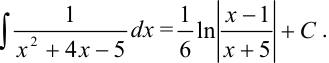 
1.3. Для нахождения интегралов вида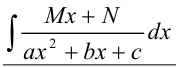 
(
, 
— 
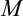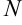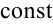) будем применять следующий алгоритм:
- Выделим в знаменателе полный квадрат.
- Выражение, стоящее в скобках, обозначим новой переменной
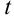. Найдем 
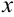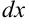, и подставим их вместе с 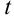в исходный интеграл (получим интеграл, содержащий только переменную 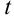). - Разобьем полученный интеграл на сумму двух интегралов, каждый из которых вычислим отдельно: один интеграл решается методом подстановки, второй сводится к одной из формул 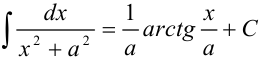или .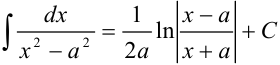
Пример №20.3.
Найдите интеграл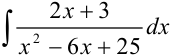 
.
Решение:
1. Попытаемся выделить в знаменателе полный квадрат. Для этого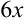 
представляем как удвоенное произведение 
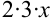. Тогда к выражению 
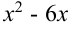следует добавить квадрат числа три, т.е. число 9: 
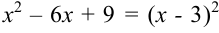. Но, чтобы выражение в знаменателе не изменилось, нужно из 
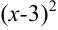вычесть 9. Получим цепочку преобразований:
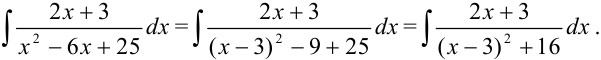
2. Введем следующую подстановку: пусть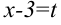 
(значит, 
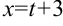), тогда 
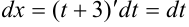. Подставим 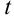, , 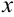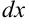в интеграл 
:
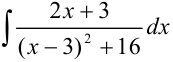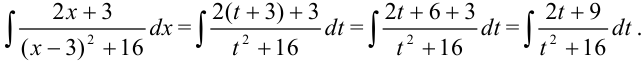
3. Представим полученный интеграл как сумму двух интегралов:
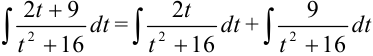. Найдем их отдельно.
3.1 Первый интеграл вычисляется методом подстановки. Обозначим знаменатель дроби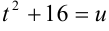 
, тогда 
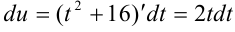. Отсюда 
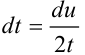. Подставляем и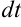 
в интеграл 
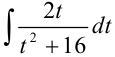и приводим его к виду: 
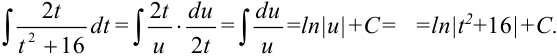Осталось вернуться к переменной 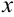. Поскольку 
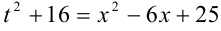, то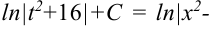 
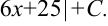
3.2 Второй интеграл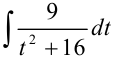 
вычисляется по формул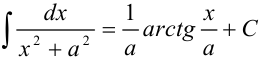е: (где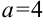 
). Тогда 
.
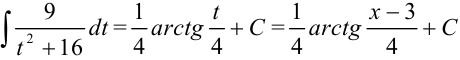3.3 Исходный интеграл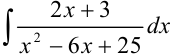 
равен сумме интегралов, найденных в пунктах 3.1 и 3.2: 
.
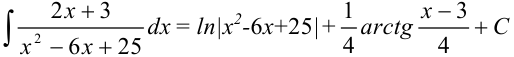Ответ: .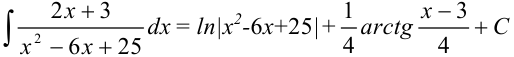
Методы интегрирования других рациональных функций рассматриваются в полном курсе математического анализа (см., например, Письменный Д.Т. Конспект лекций по высшей математике, ч.1- М.:Айрис-пресс, 2006.).
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Интегрирование методом замены переменной (методом подстановки). |
| Метод интегрирования по частям. |
| Интегрирование некоторых иррациональных функций. |
| Универсальная тригонометрическая подстановка. |
