Схему исследования функции и построения графика:
1. Найти область определения функции.
2. Исследовать функцию на четность-нечетность:
- если
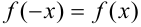, то функция четная (график четной функции симметричен относительно оси 
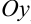); - если
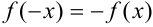, то функция нечетная (график нечетной функции симметричен относительно начала координат); - в противном случае функция ни четная, ни нечетная.
3. Исследовать функцию на периодичность (среди изучаемых нами функций периодическими могут быть только тригонометрические функции).
4. Найти точки пересечения графика функции с осями координат:
: 
(решаем уравнение лишь в том случае, если можем использовать известные нам методы);- :
.
5. Найти первую производную функции и критические точки первого рода.
6. Найти интервалы монотонности и экстремумы функции.
7.Найти вторую производную функции и критические точки второго рода.
8. Найти интервалы выпуклости-вогнутости графика функции и точки перегиба.
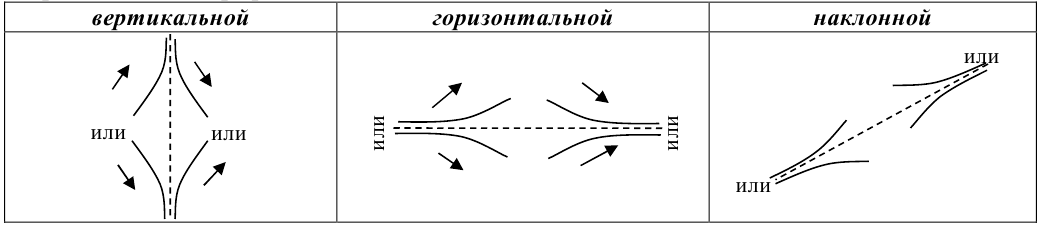
9. Найти асимптоты графика функции.
10. Построить график функции. При построении следует учесть случаи возможного расположения графика вблизи асимптот:
11. При необходимости выбрать контрольные точки для более точного построения.
Рассмотрим схему исследования функции и построения ее графика на конкретных примерах:
Пример №17.1.
Постройте график функции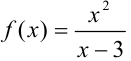 
.
Решение:
1. Данная функция определена на всей числовой прямой за исключением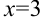 
, т.к. в этой точке знаменатель обращается в ноль.
2. Для определения четности и нечетности функции найдем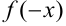 
:
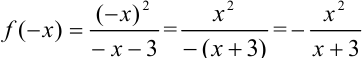. Видим, что 
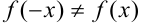и 
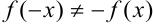, следовательно, функция 
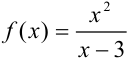ни четная, ни нечетная.
3.Функция непериодическая.
4. Найдем точки пересечения с осями координат. Для нахождения точки пересечения с осью 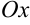примем 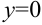. Получим уравнение: 
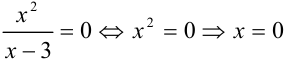. Итак, точка 
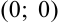— точка пересечения с осями координат.
5. Найдем производную функции по правилу дифференцирования дроби:
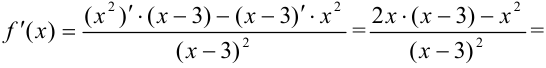
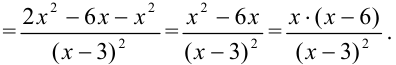
Для нахождения критических точек найдем точки, в которых производная функции равна 0 или не существует.
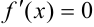, если 
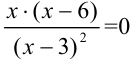, следовательно, 
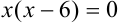. Произведение тогда равно 0, когда хотя бы один из множителей равен 0: 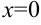или 
.
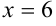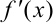не существует, если знаменатель 
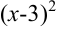равен 0, т.е. 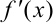не существует при .
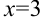Итак, функция имеет три критические точки первого рода: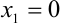 
; 
; 
.
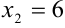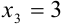6. На числовой оси отметим критические точки первого рода, причем точку 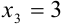отмечаем выколотой точкой, т.к. в ней функция не определена.
Расставляем знаки производной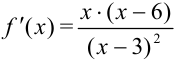 
на каждом промежутке:
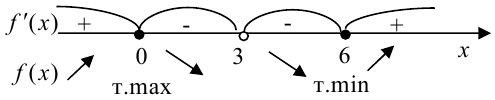
На промежутках, где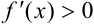 
, исходная функция возрастает (при 
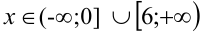), где 
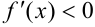— убывает (при 
).
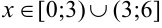Точка 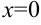является точкой максимума функции. Для нахождения максимума функции найдем значение функции в точке 0: 
.
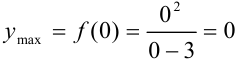Точка 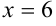является точкой минимума функции. Для нахождения минимума функции найдем значение функции в точке 6: 
.
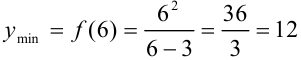Результаты исследований можно занести в таблицу. Число строк в таблице фиксировано и равно четырем, а число столбцов зависит от исследуемой функции. В ячейки первой строки последовательно заносят интервалы, на которые критические точки разбивают область определения функции, включая сами критические точки. Во избежание ошибок при построении точки, не принадлежащие области определения, можно в таблицу не включать.
Во второй строке таблицы расставляются знаки производной на каждом из рассматриваемых промежутков и значение производной в критических точках. В соответствии со знаками производной функции в третьей строке отмечаются промежутки возрастания, убывания, экстремумы функции.
Последняя строка служит для обозначения максимума и минимума функции.
7. Найдем вторую производную функции как производную от первой производной:
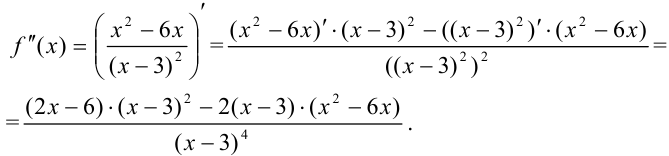
Вынесем в числителе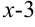 
за скобки и выполним сокращение:
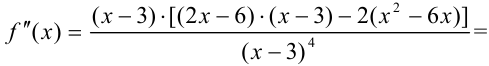
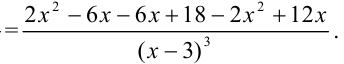
Приведем в числителе подобные слагаемые: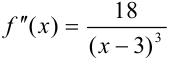 
.
Найдем критические точки второго рода: точки, в которых вторая производная функции равна нулю или не существует.
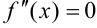, если 
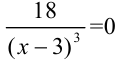. Данная дробь не может равняться нулю, следовательно, точек, в которых вторая производная функции равна нулю, нет.
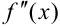не существует, если знаменатель 
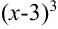равен 0, т.е. 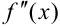не существует при .
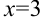Итак, функция имеет одну критическую точку второго рода: .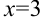
8. Найдем интервалы выпуклости и точки перегиба графика функции.
На числовой оси отметим критическую точку второго рода выколотой точкой, т.к. в ней функция не определена.
Расставляем знаки второй производной 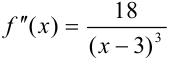на каждом промежутке:
На промежутках, где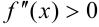 
, исходная функция вогнута (при 
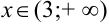), где 
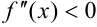— выпукла (при 
).
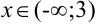Точка 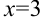не является точкой перегиба графика функции, т.к. в ней исходная функция не определена.
9. Найдем асимптоты графика функции.
9.1. Поскольку область определения функции — все действительные числа за исключением 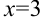, то проверим, является ли прямая 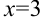вертикальной асимптотой. Для этого вычислим предел функции 
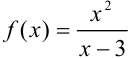в точке : 
.
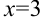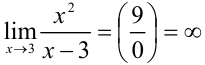Получили, что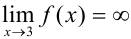 
, следовательно, 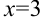— вертикальная асимптота.
9.2. Для поиска горизонтальных асимптот находим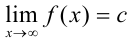 
: 
.
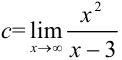Поскольку в пределе фигурирует неопределенность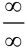 
, воспользуемся правилом Лопиталя: 
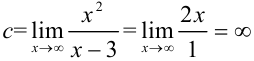. Т.к. 
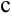— бесконечность, то горизонтальных асимптот нет.
9.3. Для поиска наклонных асимптот находим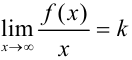 
:
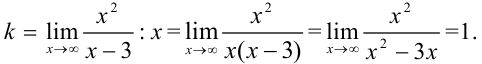
Итак,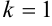 
. Найдем 
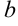по формуле: 
.
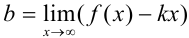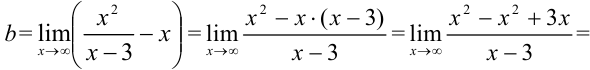
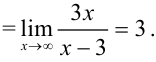
Получили, что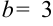 
. Тогда 
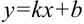— наклонная асимптота. В нашем случае она имеет вид: 
.
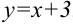Таким образом, данная функция имеет вертикальную асимптоту 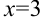и наклонную асимптоту .
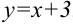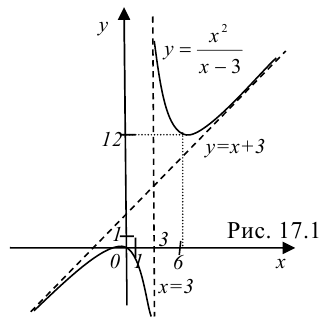
10. По полученным ранее данным строим график функции (рис. 17.1). Поскольку к построению графика предъявляются высокие требования, система координат должна быть задана корректно: должно присутствовать обозначение осей , , начало отсчета, единицы измерения по каждой оси.
Прежде чем строить график функции, нужно:
- провести асимптоты пунктирными линиями;
- отметить точки пересечения с осями координат;
- отметить максимум и минимум функции, причем рекомендуется прямо на чертеже обозначить максимум и минимум функции дугами:
или 
; - пользуясь полученными данными о промежутках возрастания, убывания, выпуклости и вогнутости, построить график функции. Ветви графика должны «стремиться» к асимптотам, но их не пересекать;
- проверить, соответствует ли график функции проведенному исследованию: если функция четная или нечетная, то соблюдена ли симметрия; соответствуют ли теоретически найденным промежутки возрастания и убывания, выпуклости и вогнутости, точки перегиба.
11. Для более точного построения можно выбрать несколько контрольных точек. Например, найдем значения функции в точках -2 и 7:
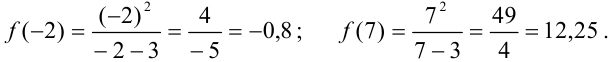
Корректируем график с учетом контрольных точек.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие асимптот |
| Алгоритм поиска асимптот |
| Понятие неопределенного интеграла. |
| Основные свойства неопределенного интеграла. |
