Оглавление:
Интервалы выпуклости и вогнутости функции находят с помощью следующей теоремы:
Теорема. 1. Если функция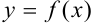 
имеет положительную вторую производную, то график функции на интервале 
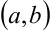вогнутый.
2. Если функция 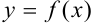имеет отрицательную вторую производную, то график функции на интервале 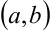выпуклый.
Представим критерий выпуклости-вогнутости функции в виде схемы:
Таким образом, исследовать функцию на выпуклость-вогнутость означает найти те интервалы области определения, в которых вторая производная сохраняет свой знак.
Заметим, что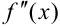 
может менять свой знак лишь в тех точках, в которых вторая производная равна нулю или не существует. Такие точки принято называть критическими точками второго рода.
Только критические точки могут быть точками перегиба. Для их нахождения используется следующая теорема:
Теорема (достаточное условие существования точек перегиба). Если вторая производная 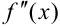при переходе через точку 
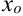меняет знак, то точка графика с абсциссой 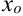является точкой перегиба.
При исследовании функции 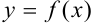на выпуклость-вогнутость и точки перегиба можно использовать следующий алгоритм:
- Найти область определения функции.
- Найти первую производную функции
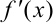. - Найти вторую производную функции .
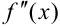- Определить критические точки второго рода (
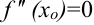или 
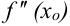не существует). - На числовой оси отметить критические точки второго рода и определить знаки второй производной на каждом из получившихся интервалов.
- Найти интервалы выпуклости-вогнутости графика функции, используя соответствующие критерии; выписать абсциссы точек перегиба (если они есть) и значение функции в этих точках.
Пример №15.1.
Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции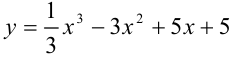 
.
Решение:
1. Данная функция определена на множестве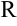 
.
2. Найдем первую производную функции: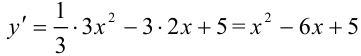 
.
3. Найдем вторую производную функции: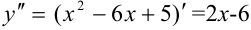 
.
4. Определим критические точки второго рода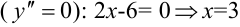 
.
5. На числовой оси отметим критическую точку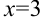 
. Она разбивает область определения функции на два интервала 
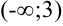и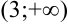 
. Расставим знаки второй производной функции 
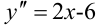на каждом из полученных интервалов:
при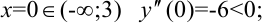 
при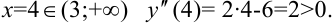 
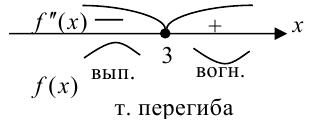
6. Согласно критерию выпуклости-вогнутости график функции 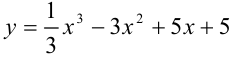выпуклый при 
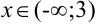, вогнутый при 
.
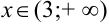Значение 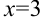— абсцисса точки перегиба. Вычислим значение функции при :
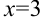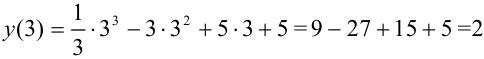. Итак, точка с координатами 
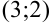— точка перегиба.
Ответ: график функции 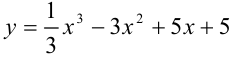выпуклый при 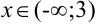, вогнутый при 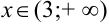; 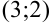— точка перегиба.
Пример №15.2.
Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции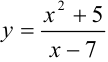 
. .
Решение:
1. Данная функция определена в том случае, когда знаменатель отличен от нуля: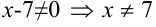 
.
2. Найдем первую производную функции:
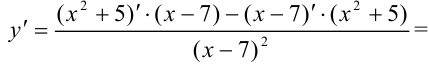
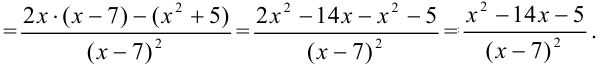
3. Найдем вторую производную функции: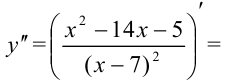 
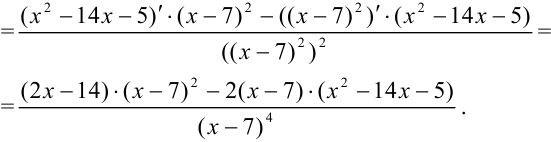
4. Вынесем в числителе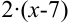 
за скобки:
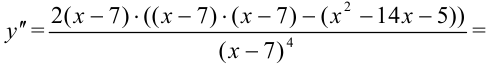
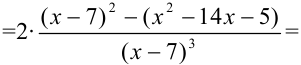
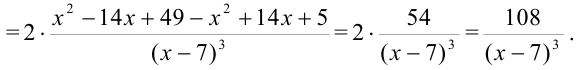
4. Определим критические точки второго рода: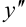 
не может быть равна нулю, поскольку числитель дроби 
.
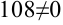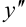не существует, если 
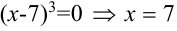— критическая точка второго рода.
5. На числовой оси отметим критическую точку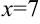 
выколотой точкой, поскольку в этой точке функция 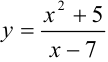не определена. Эта точка разбивает область определения функции на два интервала 
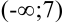и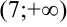 
. Расставим знаки второй производной функции 
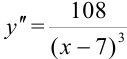на каждом из полученных интервалов:
при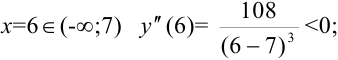 
при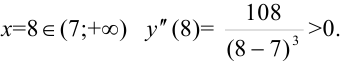 
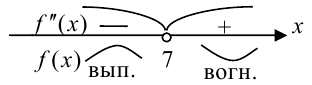
6. Согласно критерию выпуклости-вогнутости график функции 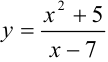является выпуклым при 
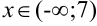, вогнутым при 
.
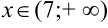Точка с абсциссой 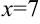не может быть точкой перегиба, т.к. в этой точке функция не существует (терпит разрыв).
Ответ: график функции 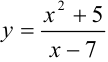выпуклый при 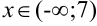, вогнутый при .
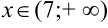Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Достаточные условия существования экстремума |
| Понятие выпуклой и вогнутой функции |
| Понятие асимптот |
| Алгоритм поиска асимптот |
