При исследовании функции бывает полезно установить, на каких промежутках функция выпуклая, а на каких — вогнутая.
Для определения выпуклой и вогнутой функции проведем касательные к графикам функции в произвольных точках  и
и  (рис. 15.1 и 15.2):
(рис. 15.1 и 15.2):
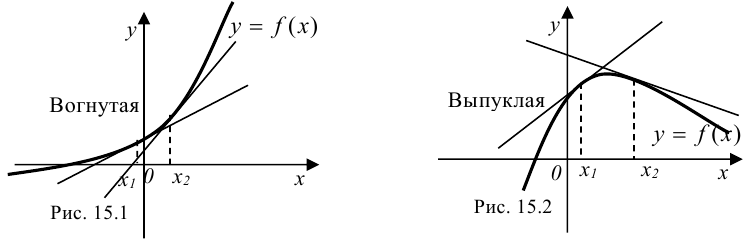
График функции 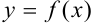 называется вогнутым на интервале
называется вогнутым на интервале 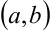 , если он расположен выше любой касательной к графику функции на данном интервале.
, если он расположен выше любой касательной к графику функции на данном интервале.
График функции 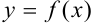 называется выпуклым на интервале
называется выпуклым на интервале 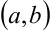 , если он расположен ниже любой касательной к графику функции на данном интервале.
, если он расположен ниже любой касательной к графику функции на данном интервале.
Точка графика непрерывной функции, в которой меняется характер выпуклости, называется точкой перегиба. В точке перегиба касательная будет пересекать кривую.
Функция может иметь несколько интервалов выпуклости и вогнутости, несколько точек перегиба. При определении промежутков выпуклости и вогнутости в качестве ответа выбирают интервал значений: точки перегиба не относят ни к промежуткам выпуклости, ни к промежуткам вогнутости.
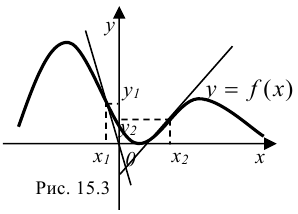
Так, график функции на рис.15.3 является выпуклым на промежутках 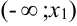 и
и 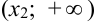 ; вогнутым на
; вогнутым на 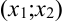 . График функции имеет две точки перегиба:
. График функции имеет две точки перегиба: 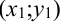 и
и 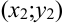 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Необходимые условия существования экстремума |
| Достаточные условия существования экстремума |
| Критерий выпуклости-вогнутости функции и точек перегиба. |
| Понятие асимптот |
