Среди всех точек области определения функции наибольший интерес для нас будут представлять точки экстремума функции.
Введем понятие окрестности. Окрестностью точки будем называть любой интервал  , содержащий эту точку.
, содержащий эту точку.
Точка 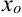 из области определения функции
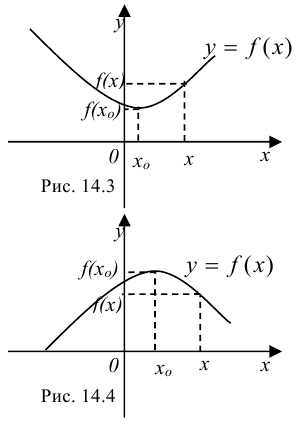
из области определения функции  называется точкой минимума функции, если для всех
называется точкой минимума функции, если для всех  из некоторой окрестности точки
из некоторой окрестности точки 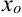 выполнено неравенство:
выполнено неравенство: 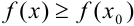 (рис. 14.3).
(рис. 14.3).
Точка 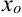 из области определения функции
из области определения функции 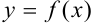 называется точкой максимума функции, если для всех
называется точкой максимума функции, если для всех  из некоторой окрестности точки
из некоторой окрестности точки 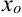 выполнено неравенство:
выполнено неравенство: 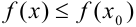 (рис. 14.4).
(рис. 14.4).
Значения функции в точках минимума и максимума называются соответственно минимумом и максимумом функции.
Точки минимума и максимума называются точками экстремума функции, а максимум и минимум — экстремумами функции.
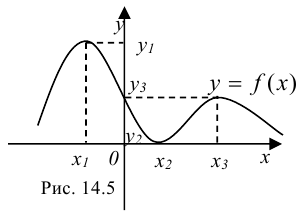
Функция может иметь несколько экстремумов.
Так, функция на рис. 14.5 имеет три точки экстремума ( — точки максимума,
— точки максимума, 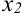 — точка минимума) и, соответственно, три экстремума (
— точка минимума) и, соответственно, три экстремума (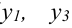 — максимумы функции,
— максимумы функции, 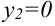 — минимум).
— минимум).
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Правило Лопиталя |
| Признаки возрастания и убывания функции |
| Необходимые условия существования экстремума |
| Достаточные условия существования экстремума |
