Напомним определение возрастающей и убывающей функции на интервале 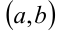 .
.
Функция 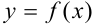 называется возрастающей на интервале
называется возрастающей на интервале 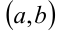 , если большему значению аргумента соответствует большее значение функции, т.е. если
, если большему значению аргумента соответствует большее значение функции, т.е. если 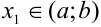 ,
, 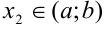 ,
, 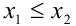 , то
, то 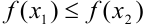 .
.
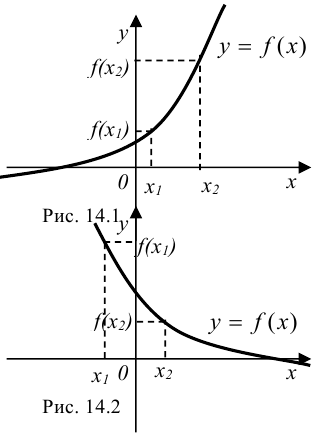
Пример возрастающей функции приведен на рис. 14.1.
Функция 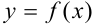 называется убывающей на интервале
называется убывающей на интервале 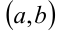 , если большему значению аргумента соответствует большее значение функции, т.е. если
, если большему значению аргумента соответствует большее значение функции, т.е. если 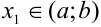 ,
, 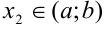 ,
, 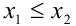 , то
, то 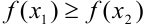 .
.
Пример убывающей функции приведен на рис. 14.2.
Интервалы, в которых функция либо только возрастает, либо только убывает, называются интервалами монотонности.
Сформулируем критерий возрастания и убывания функции:
Теорема. Пусть 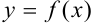 — дифференцируемая на интервале
— дифференцируемая на интервале 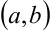 функция. Функция
функция. Функция 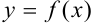 возрастает на
возрастает на 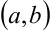 тогда и только тогда, когда её производная больше или равна нулю в любой точке этого промежутка.
тогда и только тогда, когда её производная больше или равна нулю в любой точке этого промежутка.
Функция 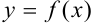 убывает на
убывает на 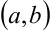 тогда и только тогда, когда ее производная меньше или равна нулю в любой точке этого промежутка.
тогда и только тогда, когда ее производная меньше или равна нулю в любой точке этого промежутка.
Представим критерий возрастания и убывания функции в виде схемы:
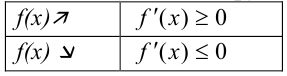
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие дифференциала высших порядков |
| Правило Лопиталя |
| Понятие точек экстремума и экстремумов функции |
| Необходимые условия существования экстремума |
