С помощью производных высших порядков вводятся дифференциалы высших порядков. Как и производные, они определяются последовательно.
Так второй дифференциал 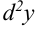 есть дифференциал от первого дифференциала,
есть дифференциал от первого дифференциала, 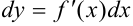 при том же самом приращении
при том же самом приращении 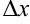 .
.
Таким образом, 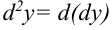 или
или 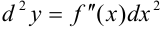 .
.
Аналогично 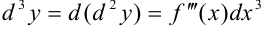 ;
;
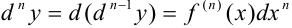
Итак, дифференциалом 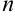 -го порядка от функции
-го порядка от функции 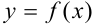 называется дифференциал от дифференциала порядка
называется дифференциал от дифференциала порядка 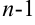 при одном и том же приращении
при одном и том же приращении 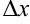 .
.
Рассмотрим пример нахождения дифференциала функции:
Пример №13.4.
Найдите дифференциал четвертого порядка функции 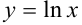 .
.
Решение:
Найдем 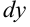 по формуле
по формуле 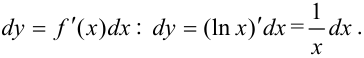
Найдем 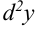 пo формуле
пo формуле 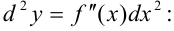
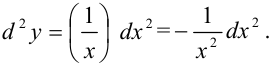 Для удобства нахождения последующих дифференциалов представим
Для удобства нахождения последующих дифференциалов представим 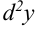 как
как 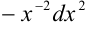 .
.
Тогда 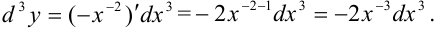
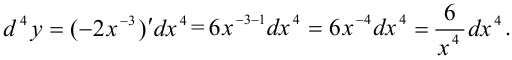
Ответ: 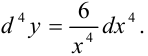
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Геометрический смысл дифференциала. |
| Понятие производной высших порядков |
| Правило Лопиталя |
| Признаки возрастания и убывания функции |

