Понятие производной высших порядков

Пусть 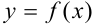— дифференцируемая на интервале 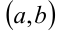функция. Тогда ее производная 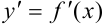— тоже функция, определенная на интервале 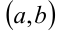. И у нее можно найти производную, называемую производной второго порядка или второй производной. Итак, производная от первой производной 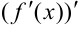называется второй производной функции и обозначается 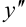или .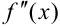

Пример №13.1.

Найдите вторую производную функции .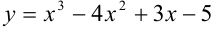

Решение:

Найдем .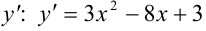

Найдем 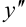как производную от .

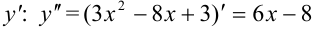Ответ: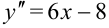

Видим, что вторая производная — тоже функция, следовательно, существует производная второй производной 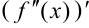, называемая третьей производной или 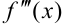. Так, в примере 13.1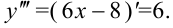

Аналогично вводится определение четвертой производной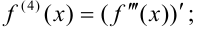

пятой производной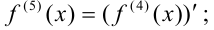

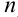-й производной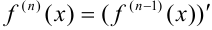

Таким образом, производной 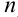-го порядка функции 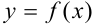называется производная от производной 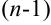-го порядка (если она существует).

Пример №13.2.

Найдите четвертую производную функции .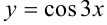

Решение:

Найдем 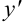как производную сложной функции :

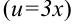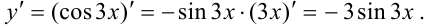
Найдем 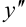как производную от :

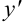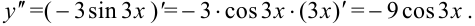
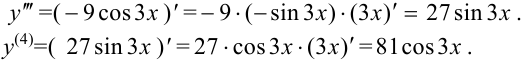
Ответ: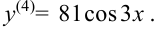

Пример №13.3.

Найдите 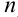-ю производную функции .

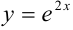Решение:

Найдем 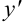как производную сложной функции :

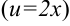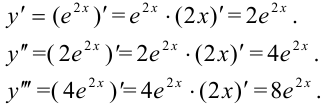
Очевидно, что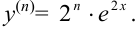

Ответ: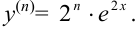

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Понятие дифференциала функции.

Геометрический смысл дифференциала.

Понятие дифференциала высших порядков

Правило Лопиталя