Пусть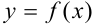 
— дифференцируемая в точке 
функция, график которой изображен на рис. 12.2. Отметим на графике точку 
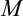, абсцисса которой равна . В точке 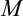проведем касательную 
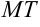к графику функции .
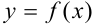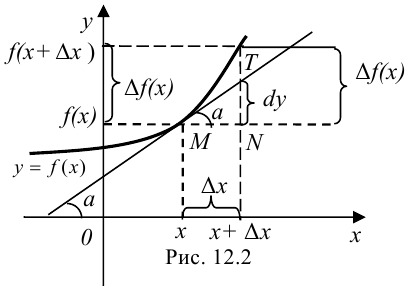
Дадим аргументу приращение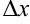 
. Из полученной точки восстановим перпендикуляр до пересечения с касательной (точка 
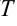) и с графиком функции 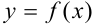. Отметим на чертеже приращение аргумента 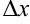(совпадает с длиной отрезка 
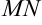) и приращение функции 
.
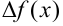Покажем, что дифференциал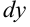 
будет совпадать с длиной отрезка 
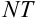. Рассмотрим треугольник 
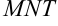— прямоугольный (по построению), 
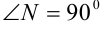. В этом треугольнике 
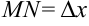, a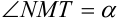 
. Выразим сторону 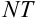через 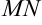и угол 
: 
.
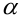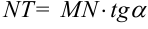В силу геометрического смысла производной тангенс угла 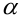, который образует касательная с положительным направлением оси 
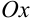, равен значению производной функции 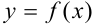в точке : 
.
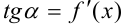Поскольку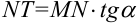 
, то 
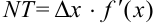, а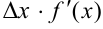 
есть ни что иное, как дифференциал 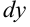. Получили, что 
.
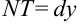Сформулируем геометрический смысл дифференциала: дифференциал функции 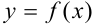в точке равен приращению ординаты касательной, проведенной к графику этой
функции в точке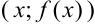 
.
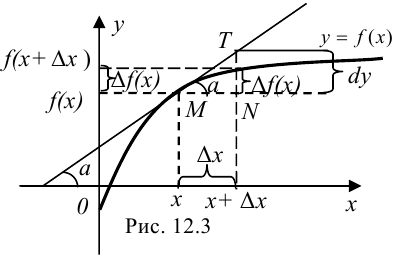
Мы рассмотрели геометрический смысл дифференциала вогнутой функции. Можно показать, что для выпуклой функции (рис. 12.3) геометрический смысл дифференциала останется таким же. Отличие будет лишь в том, что дифференциал 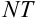окажется больше приращения функции.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Уравнение касательной к кривой. |
| Понятие дифференциала функции. |
| Понятие производной высших порядков |
| Понятие дифференциала высших порядков |
