Составим уравнение касательной, проведенной к графику функции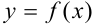 
в точке 
.
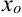Нам известны координаты точки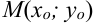 
и угловой коэффициент прямой 
.
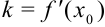Тогда уравнение прямой, проходящей через точку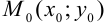
с данным угловым коэффициентом 
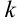, имеет вид (лекция 6): 
.
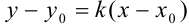Получили, что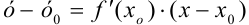 
— уравнение касательной, проведенной к графику функции 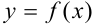в точке .
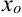Пример №12.2.
Составьте уравнение касательной, проведенной к графику функции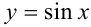 
в точке 
.
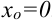Решение:
Для составления уравнения касательной удобно использовать следующую схему: 1.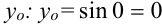 
.
2. Найдём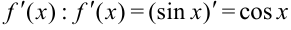 
.
3. Вычислим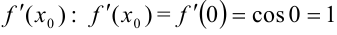 
.
4. Подставим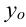 
и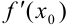 
в уравнение касательной: 
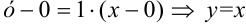— уравнение касательной, проведенной к графику функции 
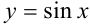в точке .
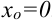Ответ: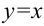 
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Производная сложной функции. |
| Геометрический смысл производной. |
| Понятие дифференциала функции. |
| Геометрический смысл дифференциала. |
