Геометрический смысл производной связан с понятием касательной.
Рассмотрим функцию 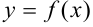 — непрерывную на отрезке
— непрерывную на отрезке 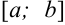 . Выберем на графике точку
. Выберем на графике точку 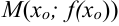 и произвольную точку
и произвольную точку 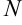 ; проведем секущую
; проведем секущую 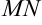 (рис. 12.1).
(рис. 12.1).
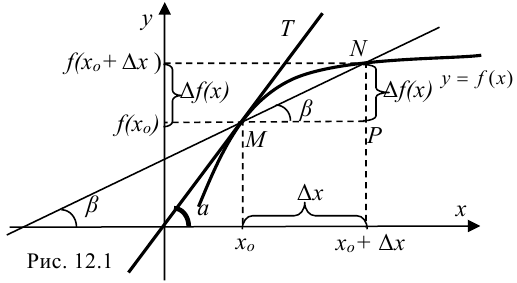
Касательной к графику функции 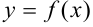 в точке
в точке 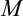 будем называть предельное положение секущей
будем называть предельное положение секущей 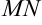 , когда точка
, когда точка 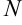 , двигаясь по кривой, стремится к точке
, двигаясь по кривой, стремится к точке 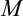 .
.
Если на рис. 12.1 провести вспомогательный отрезок 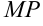 и рассмотреть прямоугольный треугольник
и рассмотреть прямоугольный треугольник 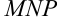 , то длина стороны
, то длина стороны 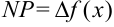 , а
, а 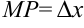 . Найдем
. Найдем 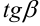 как отношение противолежащего катета к прилежащему:
как отношение противолежащего катета к прилежащему: 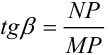 .
.
Тогда 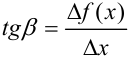 .
.
Мы нашли 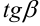 . Как же теперь осуществить переход к углу
. Как же теперь осуществить переход к углу 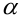 , который образует касательная с положительным направлением оси
, который образует касательная с положительным направлением оси 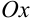 ? Очевидно, что если
? Очевидно, что если 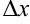 будет стремиться к 0, то угол
будет стремиться к 0, то угол 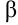 будет стремиться к углу
будет стремиться к углу 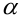 . Эта же связь будет соблюдаться и для тангенсов углов
. Эта же связь будет соблюдаться и для тангенсов углов 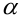 и
и 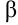 , т.е.
, т.е. 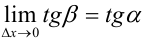 . Найдем предел
. Найдем предел 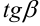 :
: 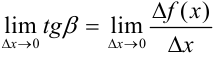 , a полученный предел есть ни что иное, как значение производной в точке
, a полученный предел есть ни что иное, как значение производной в точке 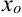 .
.
Таким образом, 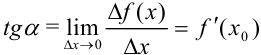 . Кроме того, касательная — прямая с угловым коэффициентом
. Кроме того, касательная — прямая с угловым коэффициентом 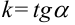 . Тогда геометрический смысл производной можно сформулировать следующим образом:
. Тогда геометрический смысл производной можно сформулировать следующим образом:
Производная функции 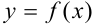 в точке
в точке 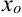 равна угловому коэффициенту касательной, проведенной к графику функции в точке
равна угловому коэффициенту касательной, проведенной к графику функции в точке 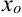 , и равна тангенсу угла наклона, который образует касательная с положительным направлением оси
, и равна тангенсу угла наклона, который образует касательная с положительным направлением оси 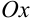 :
: 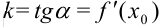 .
.
Геометрический смысл производной широко применяется при решении задач.
Пример №12.1.
Найдите угол, образованный касательной к графику функции 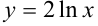 в точке
в точке 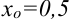 с осью абсцисс.
с осью абсцисс.
Решение:
Воспользуемся геометрическим смыслом производной: 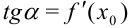 .
.
Найдем 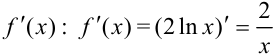 .
.
Вычислим значение производной функции в точке 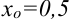 :
: 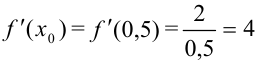 .
.
Получили, что 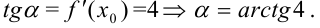
Ответ: 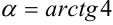 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Правила дифференцирования функций. |
| Производная сложной функции. |
| Уравнение касательной к кривой. |
| Понятие дифференциала функции. |

